Next: Nutación del giroscopio
Up: EL GIROSCOPIO
Previous: Introducción a las leyes

El aparato que vamos a estudiar consta de las siguiente partes:
- Una base con un soporte vertical que sostiene un eje por un
punto de apoyo O fijo.
Este eje está articulado en O y puede cambiar su inclinación.
- Un disco vertical grande y pesado (para que así su momento
de inercia sea grande) que gira en torno a un eje que pasa por su centro.
Este disco es el giroscopio.
- Un contrapeso al otro lado del eje para que así el eje se
pueda mantener horizontal en equilibrio.
Cuando esto ocurre podemos afirmar que el centro de masas (o centro de
gravedad) del sistema se halla colocado justo encima del punto O
que es el soporte del eje.
- Una pesa A que se colocará en uno u otro de los extermos
del eje para que así el centro de masas ya no esté
encima de O sino desplazado fuera de la vertical del soporte.
Por ser el disco grande y masivo, el momento de inercia del giroscopio con
respecto al eje que pasa por el centro del disco es mayor
que con respecto a un eje vertical cualquiera (por ejemplo, el que
pasa por el punto de apoyo O y que aparece con línea
discontinua en la figura).
Si además nos aseguramos que el disco gira con una velocidad angular
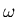 muy grande en torno al eje que pasa por el centro del disco,
entonces la componente del momento angular que va paralela a este eje
es mucho mayor que el resto de las otras componentes de
momento angular (acuérdate de que el momento angular, por ser un
vector, tiene tres componentes dirigidas cada una a lo largo de tres
ejes perpendiculares entre sí), siendo estas componentes por lo
tanto despreciables en primera aproximación.
Si se cumple entonces que el disco y que
muy grande en torno al eje que pasa por el centro del disco,
entonces la componente del momento angular que va paralela a este eje
es mucho mayor que el resto de las otras componentes de
momento angular (acuérdate de que el momento angular, por ser un
vector, tiene tres componentes dirigidas cada una a lo largo de tres
ejes perpendiculares entre sí), siendo estas componentes por lo
tanto despreciables en primera aproximación.
Si se cumple entonces que el disco y que 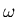 son grandes,
podemos considerar que el momento angular es prácticamente sólo su
componente paralela al eje del giroscopio y con ello que el momento
angular es paralelo al vector velocidad angular
son grandes,
podemos considerar que el momento angular es prácticamente sólo su
componente paralela al eje del giroscopio y con ello que el momento
angular es paralelo al vector velocidad angular 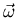 del
disco (recuerda la
regla de la mano derecha
para el vector velocidad angular).
del
disco (recuerda la
regla de la mano derecha
para el vector velocidad angular).
Nota que si, por ejemplo, el eje del giroscopio estuviera horizontal y
girara en un plano paralelo al suelo (es decir, en torno a un eje
vertical como el de la línea discontinua) a una velocidad angular
 que fuera también grande, a pesar de que el momento de
inercia del disco con respecto a este eje vertical es bastante menor
que con respecto al eje horizontal, sí podría ocurrir que la
componente del momento angular (que es el producto del momento de
inercia y la velocidad angular) a lo largo de este eje vertical ya no
fuera tan despreciable.
que fuera también grande, a pesar de que el momento de
inercia del disco con respecto a este eje vertical es bastante menor
que con respecto al eje horizontal, sí podría ocurrir que la
componente del momento angular (que es el producto del momento de
inercia y la velocidad angular) a lo largo de este eje vertical ya no
fuera tan despreciable.
Resumiendo:
El porqué de insistir tanto en que el momento angular resulte ser
paralelo al eje del giroscopio es algo que, si has entendido el final de la
introducción de Mecánica en la sección anterior, ya te lo
habrás supuesto: si el momento de las fuerzas exteriores resulta
tener dirección perpendicular al eje del giroscopio (como así va
a ser para el giroscopio), el módulo del momento angular del sistema
va a permanecer constante al ser perpendicular también al momento
angular.
Veamos que conclusiones se sacan de esta propiedad.
En lo que sigue, la notación
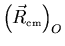 significa el vector de posición del centro de masas medido desde
O.
Mirando el siguiente dibujo vemos que
significa el vector de posición del centro de masas medido desde
O.
Mirando el siguiente dibujo vemos que
si la función del contrapeso era ``colocar'' el centro de masas
justo sobre el punto de apoyo fijo O, en el momento que coloquemos la
pesa en el extremo junto al disco, este centro de masas se desplaza
hacia la derecha, fuera del punto de apoyo.
O lo que es lo mismo, el peso del sistema tiene momento con respecto
al punto O.
El momento de esta fuerza es
 y su dirección y
sentido aparecen en la figura.
De aquí deducimos lo siguiente:
y su dirección y
sentido aparecen en la figura.
De aquí deducimos lo siguiente:
- Lo primero es que el momento del peso con respecto al punto
O peso (que es el único momento que actúa, ya que la fuerza
normal que hay en el punto de apoyo O no tiene momento con
respecto a tal punto) es perpendicular al momento angular si se
cumplen las condiciones que hemos discutido más arriba.
Por lo tanto, el peso no es capaz de variar el módulo del momento
angular, sino sólo su dirección o su sentido.
- Lo segundo es que este momento del peso está contenido en un
plano paralelo al suelo.
Por lo tanto, y de acuerdo con la Ley de Newton para la dinámica de
rotación
 (se sobreentiende en lo
que resta que el momento de las fuerzas y el momento angular se miden
con respecto a O), la variación
(se sobreentiende en lo
que resta que el momento de las fuerzas y el momento angular se miden
con respecto a O), la variación
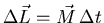 que va a poder producir este
momento del peso, al cabo de un pequeño intervalo de tiempo
que va a poder producir este
momento del peso, al cabo de un pequeño intervalo de tiempo
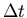 , va a ser una variación también contenida en este plano paralelo
al suelo.
En otras palabras, el momento angular va a cambiar tal y como se ve
en la siguiente figura:
, va a ser una variación también contenida en este plano paralelo
al suelo.
En otras palabras, el momento angular va a cambiar tal y como se ve
en la siguiente figura:
con
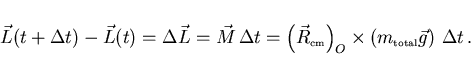 |
(17) |
Debe quedar claro (aunque en la figura por el efecto de la perspectiva
no se vea bien) que, en módulo,
 y
y
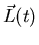 son iguales, como ya sabemos puesto que el momento del
peso es perpendicular al momento angular.
son iguales, como ya sabemos puesto que el momento del
peso es perpendicular al momento angular.
Ahora ya podemos calcular el ángulo  que se va a
desplazar el momento angular (y con él el eje del girosopio que
está horizontal) debido al momento del peso: para un intervalo de tiempo
que se va a
desplazar el momento angular (y con él el eje del girosopio que
está horizontal) debido al momento del peso: para un intervalo de tiempo
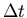 muy pequeño, de forma que
muy pequeño, de forma que  sea también muy
pequeño (mejor dicho, infinitesimal), podemos aproximar el
triángulo de la figura anterior
a un sector de círculo de radio
sea también muy
pequeño (mejor dicho, infinitesimal), podemos aproximar el
triángulo de la figura anterior
a un sector de círculo de radio
 (igualdad que ya sabemos se cumple)
y arco
(igualdad que ya sabemos se cumple)
y arco
 .
El ángulo
.
El ángulo  viene dado entonces por ``arco / radio''
viene dado entonces por ``arco / radio''
Así el ritmo con el que varía este ángulo con el tiempo,
es decir, la velocidad angular con la que el eje del giroscopio (en torno
al que está girando el disco) gira a su vez en torno a un eje
vertical que pasa por O es igual a
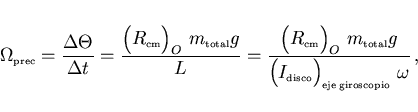 |
(18) |
con
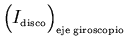 el momento de inercia del disco con respecto al eje del
giroscopio.
el momento de inercia del disco con respecto al eje del
giroscopio.
Al desplazamiento, dentro de un plano paralelo al suelo, del extremo
del eje del giroscopio se le llama precesión; y a la
velocidad angular (18), velocidad angular de precesión.
El sentido de esta precesión lo marca el sentido del momento del
peso.
De la fórmula obtenida se deduce que:
- Cuanto más se haya desplazado el centro de masas del punto de
apoyo O, es decir, cuanto mayor sea
 , más
rápidamente precede el giroscopio.
Esto es algo que ya sabemos para el caso de una bicicleta:
cuanto más nos inclinamos, y con ello más separamos nuestro centro
de gravedad (el ombligo) de la vertical que pasa por el punto de
contacto de la rueda con el suelo, más rápidamente podemos doblar
una esquina.
, más
rápidamente precede el giroscopio.
Esto es algo que ya sabemos para el caso de una bicicleta:
cuanto más nos inclinamos, y con ello más separamos nuestro centro
de gravedad (el ombligo) de la vertical que pasa por el punto de
contacto de la rueda con el suelo, más rápidamente podemos doblar
una esquina.
- Cuanto más rápido gira el disco en torno al eje del giroscopio
(es decir, cuanto mayor es
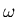 ), más lenta es la precesión.
Si alguna vez has jugado con una peonza (que no es otra cosa que un
giroscopio) ya habrás observado que al final, cuando la peonza ya ha
perdido bastante de su velocidad de giro sobre su eje de simetría,
la peonza precede mucho más rápido que al inicio (cuando se dice
que la peonza ``está dormida'').
), más lenta es la precesión.
Si alguna vez has jugado con una peonza (que no es otra cosa que un
giroscopio) ya habrás observado que al final, cuando la peonza ya ha
perdido bastante de su velocidad de giro sobre su eje de simetría,
la peonza precede mucho más rápido que al inicio (cuando se dice
que la peonza ``está dormida'').
En la siguiente película (tamaño: 1.7 MB) se puede
observar la precesión de un giroscopio para el caso que
acabamos de estudiar.
El disco del giroscopio está girando a gran velocidad en torno
a su eje que está en posición horizontal.

Movimiento de
precesión (1).
Sin embargo aquí no se acaban las cosas curiosas que hace un
giroscopio.
La siguiente cuestión es fácil de responder: qué ocurre si, con
el disco girando en torno al eje del giroscopio en el mismo sentido que
antes, ahora la pesa A que desequilibra el eje la colocamos
en el otro extremo del eje del giroscopio.
En ese caso, el centro de masas se desplaza ahora hacia la izquierda,
tal y como se ve en la
siguiente figura,
y el sentido del momento del peso es hacia afuera de esta página.
Puesto que es este momento el causante de la variación del momento
angular, éste (junto con el eje del giroscopio) va a avanzar dentro del
plano paralelo al suelo saliendo de esta página: el sentido de
precesión va es el contrario al del caso cuando la pesa A
estaba colocada en el extremo junto al disco.
La siguiente película (tamaño: 1.4 MB) muestra como
para un giroscopio cuyo disco está girando en el mismo sentido
que para la película anterior, al
colocarle la pesa A en el otro extremo del eje, el giroscopio
precede en el sentido contrario.

Movimiento de
precesión (2).
Continuemos con otra ``curiosidad''.
Hasta ahora hemos supuesto que el eje del giroscopio era paralelo al
suelo.
Si ahora este eje del giroscopio forma un ángulo  distinto
de 90 grados con la vertical, qué va a ocurrir cuando coloquemos la
pesa A que desplaza el centro de masas fuera del punto de apoyo
O.
La respuesta es que el comportamiento no se va a diferenciar en nada
de cuando el eje del giroscopio estaba horizontal.
Como podemos ver en la
siguiente figura,
distinto
de 90 grados con la vertical, qué va a ocurrir cuando coloquemos la
pesa A que desplaza el centro de masas fuera del punto de apoyo
O.
La respuesta es que el comportamiento no se va a diferenciar en nada
de cuando el eje del giroscopio estaba horizontal.
Como podemos ver en la
siguiente figura,
el momento del peso con respecto al punto de apoyo sigue siendo
perpendicular al momento angular del giroscopio; y sigue estando
contenido en un plano paralelo al suelo.
El cambio del momento angular, que sólo es un cambio en
dirección y por tanto es igual al cambio de dirección del eje del
giroscopio, es trazar un cono cuya generatriz es el propio eje del
giroscopio.
La inclinación del eje del giroscopio no es modificada por el peso.
Calcular para este caso el ángulo  que avanza el eje
del giroscopio debido al momento del peso es algo que se hace como en
el caso cuando el eje del giroscopio estaba horizontal.
Lo único es que ahora hay que tener en cuenta que el módulo del
vector momento del peso depende también de la inclinación
que avanza el eje
del giroscopio debido al momento del peso es algo que se hace como en
el caso cuando el eje del giroscopio estaba horizontal.
Lo único es que ahora hay que tener en cuenta que el módulo del
vector momento del peso depende también de la inclinación  del eje del giroscopio
del eje del giroscopio
debido a la definición del momento de una fuerza (8) como
producto vectorial.
Con ello, y teniendo el cuenta el
siguiente dibujo, se deduce
el ángulo  que, en un plano paralelo al suelo, se
desplaza o precede el eje del giroscopio al cabo de un tiempo
que, en un plano paralelo al suelo, se
desplaza o precede el eje del giroscopio al cabo de un tiempo 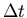 :
:
Y así la velocidad angular de precesión cuando el eje del
giroscopio está inclinado es
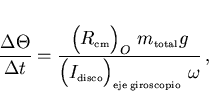 |
(19) |
que es el mismo resultado que la velocidad angular de precesión
(18) cuando el eje del giroscopio estaba horizontal.
Luego la velocidad con la que se realiza la precesión es independiente de
la inclinación que tenga el eje del giroscopio, inclinación que se
mantiene durante la precesión.



Next: Nutación del giroscopio
Up: EL GIROSCOPIO
Previous: Introducción a las leyes
José Luis Marqués 15.06.02


![]() que fuera también grande, a pesar de que el momento de
inercia del disco con respecto a este eje vertical es bastante menor
que con respecto al eje horizontal, sí podría ocurrir que la
componente del momento angular (que es el producto del momento de
inercia y la velocidad angular) a lo largo de este eje vertical ya no
fuera tan despreciable.
que fuera también grande, a pesar de que el momento de
inercia del disco con respecto a este eje vertical es bastante menor
que con respecto al eje horizontal, sí podría ocurrir que la
componente del momento angular (que es el producto del momento de
inercia y la velocidad angular) a lo largo de este eje vertical ya no
fuera tan despreciable.
![]() significa el vector de posición del centro de masas medido desde
O.
Mirando el siguiente dibujo vemos que
significa el vector de posición del centro de masas medido desde
O.
Mirando el siguiente dibujo vemos que
 (se sobreentiende en lo
que resta que el momento de las fuerzas y el momento angular se miden
con respecto a O), la variación
(se sobreentiende en lo
que resta que el momento de las fuerzas y el momento angular se miden
con respecto a O), la variación
![]() que se va a
desplazar el momento angular (y con él el eje del girosopio que
está horizontal) debido al momento del peso: para un intervalo de tiempo
que se va a
desplazar el momento angular (y con él el eje del girosopio que
está horizontal) debido al momento del peso: para un intervalo de tiempo
![]() muy pequeño, de forma que
muy pequeño, de forma que ![]() sea también muy
pequeño (mejor dicho, infinitesimal), podemos aproximar el
triángulo de la figura anterior
a un sector de círculo de radio
sea también muy
pequeño (mejor dicho, infinitesimal), podemos aproximar el
triángulo de la figura anterior
a un sector de círculo de radio
![]() (igualdad que ya sabemos se cumple)
y arco
(igualdad que ya sabemos se cumple)
y arco
![]() .
El ángulo
.
El ángulo ![]() viene dado entonces por ``arco / radio''
viene dado entonces por ``arco / radio''
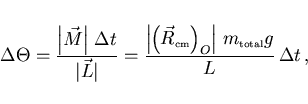


![]() distinto
de 90 grados con la vertical, qué va a ocurrir cuando coloquemos la
pesa A que desplaza el centro de masas fuera del punto de apoyo
O.
La respuesta es que el comportamiento no se va a diferenciar en nada
de cuando el eje del giroscopio estaba horizontal.
Como podemos ver en la
siguiente figura,
distinto
de 90 grados con la vertical, qué va a ocurrir cuando coloquemos la
pesa A que desplaza el centro de masas fuera del punto de apoyo
O.
La respuesta es que el comportamiento no se va a diferenciar en nada
de cuando el eje del giroscopio estaba horizontal.
Como podemos ver en la
siguiente figura,
![]() que avanza el eje
del giroscopio debido al momento del peso es algo que se hace como en
el caso cuando el eje del giroscopio estaba horizontal.
Lo único es que ahora hay que tener en cuenta que el módulo del
vector momento del peso depende también de la inclinación
que avanza el eje
del giroscopio debido al momento del peso es algo que se hace como en
el caso cuando el eje del giroscopio estaba horizontal.
Lo único es que ahora hay que tener en cuenta que el módulo del
vector momento del peso depende también de la inclinación ![]() del eje del giroscopio
del eje del giroscopio