 |
(1) |
Para explicar el giroscopio es necesario que repasemos los fundamentos
de la mecánica del sólido rígido.
Si esto ya lo conoces, puedes pasar a la
siguiente sección.
Si quieres comprobar si lo que sabes de Mecánica es suficiente para entender el funcionamiento del giroscopio, puedes hacer el siguiente TEST.
La ecuación fundamental que describe el movimiento de una partícula,
es decir de una masa lo suficientemente pequeña para que podamos
considerar que no tiene dimensiones o que sus dimensiones no juegan
ningún papel en el movimiento, es
Sin embargo, lo normal es que tengamos un cuerpo compuesto por muchas
partículas: un sistema de partículas.
Puesto que la ecuación (1) se cumple para cada una de las
partículas, sumando sobre todas estas partículas obtenemos
Para terminar de simplificar la ecuación (3) nos hace
falta obtener un resultado para el momento lineal del sistema
![]() que sea más manejable que decir que es la
suma de los momentos de todas las partículas del sistema.
Y para ello necesitamos el concepto de centro de masas o centro de gravedad.
Aunque todos tenemos una idea más o menos intuitiva de qué es el
centro de gravedad de un cuerpo (por ejemplo, el centro de gravedad
del ser humano coincide aproximadamente con el ombligo), la
definición del centro de masas (o centro de gravedad) de un sistema
de partículas es un poco más complicada.
La velocidad del centro de masas se define como la media ponderada de
la velocidad 1calculada sumando la masa de cada una de las partículas
multiplicada por su velocidad y dividido todo por la masa total del sistema
que sea más manejable que decir que es la
suma de los momentos de todas las partículas del sistema.
Y para ello necesitamos el concepto de centro de masas o centro de gravedad.
Aunque todos tenemos una idea más o menos intuitiva de qué es el
centro de gravedad de un cuerpo (por ejemplo, el centro de gravedad
del ser humano coincide aproximadamente con el ombligo), la
definición del centro de masas (o centro de gravedad) de un sistema
de partículas es un poco más complicada.
La velocidad del centro de masas se define como la media ponderada de
la velocidad 1calculada sumando la masa de cada una de las partículas
multiplicada por su velocidad y dividido todo por la masa total del sistema
Un caso distinto sería si ahora el disco horizontal ya no girara en torno a un eje que pasara por su centro, sino en torno a un eje que por ejemplo estuviera muy cerca de la periferia del disco. En tal caso la media ponderada de la velocidad ya no sería cero: hay muchos más puntos a un lado del eje que al otro y por lo tanto ya no podemos encontrar para cualquier punto del disco otro punto que lleve su misma velocidad pero en sentido contrario. Y por otro lado, si ahora soltáramos el disco, este sí se desplazaría: volvemos a ver que la media ponderada de la velocidad está relacionada con el desplazamiento del centro de gravedad del sistema de partículas.
Así, el momento lineal de todo el sistema de partículas
![]() que aparece en la ecuación
(3) se define como el producto de la masa total del sistema
de partículas por la velocidad de traslación que lleva el centro
de masas
que aparece en la ecuación
(3) se define como el producto de la masa total del sistema
de partículas por la velocidad de traslación que lleva el centro
de masas
Como acabamos de ver en el segundo ejemplo anterior, para describir completamente el movimiento de un sistema de partículas no nos vale con saber la velocidad de traslación del centro de masas: el disco puede estar girando en torno a su centro pero no desplazarse, con lo que decir que el centro de masas no se desplaza no es suficiente para describir cómo se está moviendo el disco. Nota que esto no ocurría para una única partícula, en donde hablar de giros no tiene sentido al no tener la partícula nigún tamaño o dimensiones. Para describir la dinámica de un sistema de partículas por completo hay que tener en cuenta los giros. Y para describir los giros, un elemento fundamental es saber en torno a qué eje o punto está girando el sistema de partículas (compara los dos casos vistos en el ejemplo del disco que giraba).
La capacidad que tiene una fuerza de hacer girar un cuerpo en torno a
un eje se llama el momento de la fuerza respecto a ese eje y se define
matemáticamente como el siguiente producto vectorial
y depende del ángulo ![]() que forme la fuerza con el vector de
posición que viene desde el punto O por donde pasa el eje.
La dirección y sentido del momento de la fuerza lo determinan la
regla de la mano derecha: la dirección del producto vectorial
que forme la fuerza con el vector de
posición que viene desde el punto O por donde pasa el eje.
La dirección y sentido del momento de la fuerza lo determinan la
regla de la mano derecha: la dirección del producto vectorial
![]() es perpendicular al plano donde están
contenidos los dos vectores
es perpendicular al plano donde están
contenidos los dos vectores ![]() y
y ![]() ; y el sentido del
producto vectorial es hacia donde apunte el pulgar de la mano
derecha cuando el resto de los dedos están colocados en el sentido
de giro del ángulo
; y el sentido del
producto vectorial es hacia donde apunte el pulgar de la mano
derecha cuando el resto de los dedos están colocados en el sentido
de giro del ángulo ![]() cuando se va del primer factor (esto es,
cuando se va del primer factor (esto es,
![]() ) al segundo factor (o sea,
) al segundo factor (o sea, ![]() ) de
) de
![]() , considerando este sentido de giro a lo largo
del camino más corto que una a los dos vectores que se multiplican y
tomando el sentido una vez que ``mentalmente'' hemos colocado los dos
vectores saliendo del mismo origen.
, considerando este sentido de giro a lo largo
del camino más corto que una a los dos vectores que se multiplican y
tomando el sentido una vez que ``mentalmente'' hemos colocado los dos
vectores saliendo del mismo origen.
De la misma forma que para la traslación de un sistema de partículas
es el momento lineal del sistema -- que depende de la masa y de la
velocidad de traslación -- la magnitud fundamental, en el caso
de la rotación se define una magnitud que es en parte similar: el
momento angular.
Lo mismo que el momento lineal depende de la velocidad de
traslación, el momento angular depende de la velocidad de rotación
![]() ; y también el momento angular, como el momento
lineal, depende de la masa del sistema de partículas, si bien esta
dependencia es ahora más complicada: no sólo va a depender
de la masa sino de las dimensiones del sistema de partículas (o
sea, de su forma).
La magnitud que contiene esta información sobre la masa y
dimensiones del sistema de partículas se llama momento de inercia
I, aunque ahora no necesitamos saber cómo depende exactamente
de la masa y de la forma del cuerpo.
Lo que sí que es importante, y ya te habrás ido dando cuenta, es
que todas las magnitudes que estamos definiendo para describir giros
dependen sobre todo de la posición del eje de rotación (recuerda
que para un mismo disco, no es lo mismo que gire en torno a su centro
a que lo haga en torno a un eje que pase por la periferia del disco).
Resumiendo, el momento angular de un sistema de partículas con respecto a un eje que pasa por O se define como
; y también el momento angular, como el momento
lineal, depende de la masa del sistema de partículas, si bien esta
dependencia es ahora más complicada: no sólo va a depender
de la masa sino de las dimensiones del sistema de partículas (o
sea, de su forma).
La magnitud que contiene esta información sobre la masa y
dimensiones del sistema de partículas se llama momento de inercia
I, aunque ahora no necesitamos saber cómo depende exactamente
de la masa y de la forma del cuerpo.
Lo que sí que es importante, y ya te habrás ido dando cuenta, es
que todas las magnitudes que estamos definiendo para describir giros
dependen sobre todo de la posición del eje de rotación (recuerda
que para un mismo disco, no es lo mismo que gire en torno a su centro
a que lo haga en torno a un eje que pase por la periferia del disco).
Resumiendo, el momento angular de un sistema de partículas con respecto a un eje que pasa por O se define como
Al comienzo de esta introducción se habló de la dinámica del
sólido rígido: este sólido rígido es una aproximación
ideal a un sistema de partículas que no se deformara nunca,
independientemente de la velocidad de rotación que lleve (aunque
esto no se da nunca en la Naturaleza, hasta la Tierra está deformada
debido a su propia rotación en torno a su eje).
La relación que describe los giros en un sólido rígido,
relación que completa así la información suministrada por la
ecuación (6) para la traslación, es
La siguiente tabla cuadro contiene el resumen de los resultados obtenidos para la dinámica de traslación y rotación de un sistema de partículas, y sirve para destacar la similitud que hay entre ambas dinámicas:
| Traslación | Rotación | |||
| espacio recorrido |
|
ángulo girado | ||
| velocidad lineal |
|
velocidad angular | ||
| masa del sistema |
|
momento de inercia | ||
|
|
|
||
|
|
|
Antes de acabar con esta introducción hay un punto que nos queda
todavía por tratar.
Hasta ahora hemos estado trabajando con vectores tanto fuerzas/momento
de fuerzas como momento lineal/angular.
Sin embargo la dinámica de una sistema de partículas puede ser
descrita también utilizando el concepto de energía o trabajo,
que tiene la ventaja sobre las Leyes de Newton (11) que en vez
de trabajar con vectores (para los que hay que indicar módulo,
dirección y sentido) se trabaja sólo con escalares, es decir con
números a secas.
El trabajo dW hecho por una fuerza ![]() al desplazar un
cuerpo una distancia muy pequeña
al desplazar un
cuerpo una distancia muy pequeña ![]() viene definido por el
producto escalar
viene definido por el
producto escalar
Consideremos un sólido rígido (es decir, un sistema de
partículas que nunca se deforma) desplazándose sin rotar, esto
es, cada partícula lleva la misma velocidad que el centro de
masas.
Y supongamos que actúa sobre este sistema una fuerza externa
![]() : se pregunta cómo está relacionado el
trabajo que realiza esta fuerza exterior con el momento lineal del
sistema de partículas.
De acuerdo con la Ley de Newton para el movimiento de traslación del
centro de masas tenemos que
: se pregunta cómo está relacionado el
trabajo que realiza esta fuerza exterior con el momento lineal del
sistema de partículas.
De acuerdo con la Ley de Newton para el movimiento de traslación del
centro de masas tenemos que
 , luego (12) se puede escribir como
, luego (12) se puede escribir como
 y el bloque se desplaza como un
todo con la velocidad del centro de masas
y el bloque se desplaza como un
todo con la velocidad del centro de masas
 (nota que la
velocidad del centro de masas es paralela al momento lineal del
sistema ya que la masa es un escalar, un número), tenemos que
(nota que la
velocidad del centro de masas es paralela al momento lineal del
sistema ya que la masa es un escalar, un número), tenemos que
 .
Si ahora queremos saber el trabajo realizado por la fuerza exterior no
sólo para un pequeño desplazamiento infinitesimal
.
Si ahora queremos saber el trabajo realizado por la fuerza exterior no
sólo para un pequeño desplazamiento infinitesimal  .
Fíjate que el trabajo depende de
.
Fíjate que el trabajo depende de
 no es
otra cosa que la energía cinética de traslación
no es
otra cosa que la energía cinética de traslación

Y con esto llegamos a un resultado interesante: si la fuerza exterior es
perpendicular al momento lineal del sistema de partículas,
entonces esa fuerza no realiza trabajo.
La razón es muy sencilla: puesto que como ya hemos visto se cumple que
 ,
entonces
,
entonces

O lo que es lo mismo: la energía cinética no varía si
![]() y
y
![]() son perpendiculares.
Un caso donde se da esta situación es por ejemplo en un satélite
alrededor de la Tierra: la única fuerza que actúa sobre él es la
atracción gravitatoria de la Tierra, que lleva una dirección
perpendicular a la velocidad de traslación del satélite (y por
tanto, también es perpendicular al momento lineal del satélite ya
que el momento lineal es directamente proporcional a la velocidad de
traslación del centro de masas).
Es importante insistir en que este resultado deriva de la relación
son perpendiculares.
Un caso donde se da esta situación es por ejemplo en un satélite
alrededor de la Tierra: la única fuerza que actúa sobre él es la
atracción gravitatoria de la Tierra, que lleva una dirección
perpendicular a la velocidad de traslación del satélite (y por
tanto, también es perpendicular al momento lineal del satélite ya
que el momento lineal es directamente proporcional a la velocidad de
traslación del centro de masas).
Es importante insistir en que este resultado deriva de la relación
 ,
esto es, porque
,
esto es, porque ![]() y
y
![]() son paralelos
entre sí.
Y esto se cumple siempre ya que el momento lineal del sistema es
siempre paralelo a la velocidad del centro de masas.
En esto se diferencia de la dinámica de rotación, donde tal
relación no se cumple siempre.
son paralelos
entre sí.
Y esto se cumple siempre ya que el momento lineal del sistema es
siempre paralelo a la velocidad del centro de masas.
En esto se diferencia de la dinámica de rotación, donde tal
relación no se cumple siempre.
Como ya te estarás imaginando, ahora nos queda ver qué forma tiene
el trabajo realizado por una fuerza cuando en vez de trasladar el
centro de masas lo que hace es hacer girar el sistema de partículas
alrededor de un eje.
Sin hacer la demostración matemática, sí que podemos obtener
cuál va a ser el resultado final teniendo en cuenta la
tabla anterior:
sustituimos la fuerza exterior por el momento de esta fuerza y en
cambio del pequeño (infinitesimal) desplazamiento ![]() un
pequeño ángulo girado
un
pequeño ángulo girado ![]() .
Como ya hemos visto para la velocidad angular, a este ángulo girado se
le da carácter vectorial de acuerdo con la regla de la mano derecha
(ver figura).
Obtenemos así
.
Como ya hemos visto para la velocidad angular, a este ángulo girado se
le da carácter vectorial de acuerdo con la regla de la mano derecha
(ver figura).
Obtenemos así
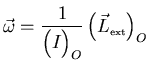 , puesto que
el momento de inercia
, puesto que
el momento de inercia

Conviene que no continúes leyendo si las ideas principales de la
introducción anterior no las has entendido.
Si quieres, puedes comprobar lo que has aprendido haciendo el
siguiente TEST.