 (masa = volumen x densidad),
hasta que choca con la masa M del péndulo balístico, la
trayectoria es prácticamente horizontal (aunque en realidad sea un
tiro parabólico).
(masa = volumen x densidad),
hasta que choca con la masa M del péndulo balístico, la
trayectoria es prácticamente horizontal (aunque en realidad sea un
tiro parabólico).
Supongamos que desde que disparamos la bolita de plomo, que tiene una
masa igual a
 (masa = volumen x densidad),
hasta que choca con la masa M del péndulo balístico, la
trayectoria es prácticamente horizontal (aunque en realidad sea un
tiro parabólico).
(masa = volumen x densidad),
hasta que choca con la masa M del péndulo balístico, la
trayectoria es prácticamente horizontal (aunque en realidad sea un
tiro parabólico).
La velocidad ![]() con la que la bolita de plomo sale disparada al
soltar el muelle (que está comprimido una distancia x) se
calcula utilizando la conservación de la energía
mecánica: antes de soltar la bolita, ésta sólo tiene energía
potencial elástica,
con la que la bolita de plomo sale disparada al
soltar el muelle (que está comprimido una distancia x) se
calcula utilizando la conservación de la energía
mecánica: antes de soltar la bolita, ésta sólo tiene energía
potencial elástica,
 , y después de que el
muelle se ha estirado completamente, la bolita sólo tiene energía
cinética (puesto que estamos suponiendo que la bolita sigue una
trayectoria horizontal, sin cambiar de altura, no hace falta que
tengamos en cuenta la energía potencial gravitatoria)
, y después de que el
muelle se ha estirado completamente, la bolita sólo tiene energía
cinética (puesto que estamos suponiendo que la bolita sigue una
trayectoria horizontal, sin cambiar de altura, no hace falta que
tengamos en cuenta la energía potencial gravitatoria)
![]() Ahora la bolita llega a la masa M del péndulo balístico,
se incrusta en ella y le comunica un impulso.
La interacción entre las dos masas (una fuerza interna al sistema
formado por bolita + péndulo balístico) no modifica el momento
angular de este sistema, por lo que podemos afirmar que que el momento
angular justo antes del choque es igual al momento justo después;
por supuesto, esta conservación del momento angular no se cumple si
entre justo antes del choque y, por ejemplo, tres minutos después de
él, ya que mientras tanto ha estado actuando la fuerza de la
gravedad que es una fuerza externa al sistema y por tanto modifica el
momento angular.
Así, con respecto al punto del techo de donde cuelga la masa M,
tenemos
Ahora la bolita llega a la masa M del péndulo balístico,
se incrusta en ella y le comunica un impulso.
La interacción entre las dos masas (una fuerza interna al sistema
formado por bolita + péndulo balístico) no modifica el momento
angular de este sistema, por lo que podemos afirmar que que el momento
angular justo antes del choque es igual al momento justo después;
por supuesto, esta conservación del momento angular no se cumple si
entre justo antes del choque y, por ejemplo, tres minutos después de
él, ya que mientras tanto ha estado actuando la fuerza de la
gravedad que es una fuerza externa al sistema y por tanto modifica el
momento angular.
Así, con respecto al punto del techo de donde cuelga la masa M,
tenemos
Para calcular ahora la altura h hasta la que suben las dos masas
utilizamos otra vez la conservación de la energía mecánica:

![]() Hemos obtenido
Hemos obtenido
 ,
o lo que es lo mismo, comparando con
,
o lo que es lo mismo, comparando con ![]() , tenemos que
, tenemos que ![]() y
y
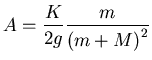 (con K y
M desconocidos).
Para determinar el valor de A (para luego poder deducir M),
vamos a representar los datos que nos dan.
La mejor forma de hacerlo es ingeniárnoslas para que la
representación gráfica resulte ser una recta: puesto que h
es proporcional a x al cuadrado, la forma de obtener una
recta es representar en un eje
(con K y
M desconocidos).
Para determinar el valor de A (para luego poder deducir M),
vamos a representar los datos que nos dan.
La mejor forma de hacerlo es ingeniárnoslas para que la
representación gráfica resulte ser una recta: puesto que h
es proporcional a x al cuadrado, la forma de obtener una
recta es representar en un eje ![]() y en el otro
y en el otro ![]() , para que
asílo representado en un eje sea linealmente proporcional a lo
representado en el otro (lo que por definición es una recta).
La pendiente de tal recta será la constante de proporcionalidad
entre
, para que
asílo representado en un eje sea linealmente proporcional a lo
representado en el otro (lo que por definición es una recta).
La pendiente de tal recta será la constante de proporcionalidad
entre ![]() y
y ![]() , o sea
, o sea ![]() ; para más detalles, ver
trucos.
; para más detalles, ver
trucos.
O, puesto que lo que nos dan es directamente el ángulo, también
podemos operar
La pendiente la podemos calcular aproximadamente midiendo el ángulo
de la recta (la pendiente es la tangente trigonométrica de este
ángulo) o bien tomando dos puntos cualesquiera de la recta: por
ejemplo con el primer y último punto de la recta se obtiene
Puesto que además nos dicen que si al muelle de constante K
desconocidad le colgamos una masa M+m y dejamos que alcance su
posición de equilibrio, el alargamiento del muelle es
![]() , entonces (ver
figura)
, entonces (ver
figura)
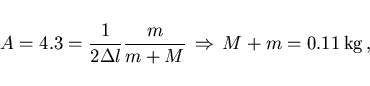
En cuanto a la última pregunta de este apartado, nuestra regla
sólo puede distinguir milímetros.
El alargamiento que produce la bolita de plomo, que tiene una masa de
0.01 kilogramos, sería de (ver (24))
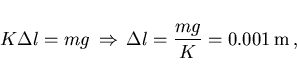
![]() Supongamos que, al no saber deducir (21), no podemos
determinar que la altura es proporcional al cuadrado de los que se ha
comprimido originariamente el muelle para disparar la bolita de plomo.
Nos encontramos con
Supongamos que, al no saber deducir (21), no podemos
determinar que la altura es proporcional al cuadrado de los que se ha
comprimido originariamente el muelle para disparar la bolita de plomo.
Nos encontramos con ![]() , pero ahora con A y también
n desconocidos.
La forma de obtener el valor del exponente en tal caso se obtiene,
como se indica en el problema, utilizando el método de tomar
logaritmos
(con más detalle en la página dedicada a
trucos):
, pero ahora con A y también
n desconocidos.
La forma de obtener el valor del exponente en tal caso se obtiene,
como se indica en el problema, utilizando el método de tomar
logaritmos
(con más detalle en la página dedicada a
trucos):

Una forma aproximada de obtener la pendiente y el término
independiente de la recta es volviendo a tomar dos puntos cualesquiera
de la recta (por ejemplo el primero y el último) y recordar que
![]()
![\begin{displaymath}
\mbox{pendiente}=n=\frac{\ln\left[L\left(1-\cos(\theta=36)\r...
...(\theta=11)\right)\right]}
{\ln (x=0.15)-\ln (x=0.05)}=2.1\, ,
\end{displaymath}](img86.png)
![\begin{displaymath}
\ln A=\ln\left[L\left(1-\cos(\theta=36)\right)\right]
-\underbrace{n}_{\displaystyle =2} \ln (x=0.15)=1.446\, ,
\end{displaymath}](img87.png)