


Next: Fase Local de La Rioja 2002
Up: Olimpiadas de Física
Descarga del contenido de esta página
aquí: apretando la tecla
derecha del ratón sobre el enlace subrayado, elegir ``Guardar enlace
como'' (Netscape) o ``Guardar objetivo como'' (Explorer).
Para usuarios de Linux, el archivo se puede abrir con el programa
GhostView: escribir gv ol_truco.pdf & o bien
kghostview ol_truco.pdf & en una consola de texto.
Para usuarios de Windows, el archivo se abre con el programa Acrobat
Reader cliqueando directamente sobre el icono del archivo.
PREPARACIÓN PARA LAS OLIMPIADAS NACIONALES
DE FÍSICA
REPASO DE MECÁNICA
Tengamos un cuerpo con dimensiones, es decir, un sistema formado por
varias masas puntuales. Si consideramos dos intantes de tiempo
diferentes  y
y  muy poco separados entre sí, se
cumple que
muy poco separados entre sí, se
cumple que
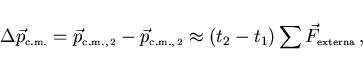 |
(1) |
donde
 es la suma de todas las
fuerzas externas al sistema;
es la suma de todas las
fuerzas externas al sistema;
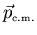 es el momento
lineal (o impulso) del centro de masas de todo el sistema y viene dado
por la masa total del sistema multiplicada por la velocidad que lleva
el centro de masas
es el momento
lineal (o impulso) del centro de masas de todo el sistema y viene dado
por la masa total del sistema multiplicada por la velocidad que lleva
el centro de masas
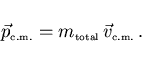 |
(2) |
Si en vez de varias masas puntuales formando un cuerpo con dimensiones
tunemos una única masa puntual, entonces el centro de masas
coincide con la masa puntual.
Volviendo a la ecuación (1), si
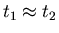 (por
ejemplo, consideramos el instante justo antes y
justo después de un choque que no dura prácticamente nada de
tiempo), entonces se cumple
(por
ejemplo, consideramos el instante justo antes y
justo después de un choque que no dura prácticamente nada de
tiempo), entonces se cumple
 , es decir,
el momento lineal del centro de masas se conserva.
Evidentemente, el momento lineal también se conserva
independientemente de lo cercano que esté
, es decir,
el momento lineal del centro de masas se conserva.
Evidentemente, el momento lineal también se conserva
independientemente de lo cercano que esté  de
de  si
si
 .
.
Si además de desplazarse el cuerpo también rota, por ejemplo en
torno a un punto O, entonces además de (1) se cumple
que para dos dos instantes  y
y  muy poco separados entre sí
muy poco separados entre sí
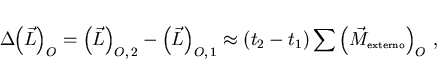 |
(3) |
donde
 es el momento
angular del sistema, medido con respecto a O, y
es el momento
angular del sistema, medido con respecto a O, y
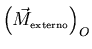 es el momento de una fuerza externa medido también con respecto a
O.
Como cuando se trabaja con momentos angulares y momentos de fuerzas es
fundamental indicar con respecto a qué punto O se están calculando
estos momentos, utilizaremos para lo que sigue la notación
es el momento de una fuerza externa medido también con respecto a
O.
Como cuando se trabaja con momentos angulares y momentos de fuerzas es
fundamental indicar con respecto a qué punto O se están calculando
estos momentos, utilizaremos para lo que sigue la notación
 para indicarlo.
para indicarlo.
El momento angular de una partícula (=masa puntual) con respecto a
un punto O se define como el producto vectorial del vector de
posición de la partícula visto desde O por el momento lineal
que lleva la partícula,
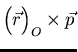 .
En el caso de un sistema de partículas, el momento angular es la
suma de los momentos angulares de cada una de las partículas; y si
además se cumple que el cuerpo es rígido (=no deformable)
entonces se puede demostrar que
.
En el caso de un sistema de partículas, el momento angular es la
suma de los momentos angulares de cada una de las partículas; y si
además se cumple que el cuerpo es rígido (=no deformable)
entonces se puede demostrar que
 se puede escribir también de la siguiente forma
se puede escribir también de la siguiente forma
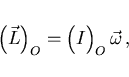 |
(4) |
donde  es la velocidad angular (su dirección marcada
por el pulgar extendido de la mano derecha cuando se ponen el resto de
los dedos plegados en la dirección de giro);
es la velocidad angular (su dirección marcada
por el pulgar extendido de la mano derecha cuando se ponen el resto de
los dedos plegados en la dirección de giro);
 es el momento de inercia del
sistema de partículas con respecto al punto O y viene definido
como la suma sobre todas las partículas del cuadrado de la
distancia de cada partícula a O multiplicado por su masa
es el momento de inercia del
sistema de partículas con respecto al punto O y viene definido
como la suma sobre todas las partículas del cuadrado de la
distancia de cada partícula a O multiplicado por su masa
Para una única partícula de masa  , su momento de inercia es
, su momento de inercia es
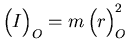 ; y por ejemplo para un
un disco macizo de masa
; y por ejemplo para un
un disco macizo de masa  y radio
y radio 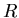 que está
girando en torno a un eje perpendicular al centro del disco O, entonces
que está
girando en torno a un eje perpendicular al centro del disco O, entonces
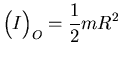 .
.
En la ecuación (3), el momento
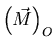 de una fuerza
de una fuerza
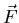 respecto a un punto O está definido por el producto
vectorial
respecto a un punto O está definido por el producto
vectorial
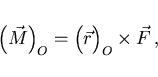 |
(5) |
siendo
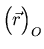 el vector de
posición que va desde el punto O hasta el punto de aplicación de
la fuerza
el vector de
posición que va desde el punto O hasta el punto de aplicación de
la fuerza 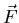 .
Las ecuaciones de la mecánica con las que estamos trabajando
``funcionan'' siempre y cuando las medidas y calculos se hagan con
respecto a un sistema inercial, es decir, con respecto a un observador
que no esté sometido a ninguna aceleración, que no esté sometido
a ninguna fuerza resultante.
Si no es así, las ecuaciones dejan de ser válidas (la única
forma de hacer que entonces las ecuaciones todavía funcionen es
introduciendo fuerzas ficticias como la fuerza de inercia o la
centrífuga).
Por ello en las ecuaciones (3) y (5), el punto
de referencia O tiene que ser un punto no sometido a ninguna
aceleración.
Hay una excepción a esta regla: por la propia definición del
centro de masas, las ecuaciones (3) y (5)
siguen siendo válidas si O corresponde al centro de masas, aunque
éste sea una punto que lleve aceleración.
.
Las ecuaciones de la mecánica con las que estamos trabajando
``funcionan'' siempre y cuando las medidas y calculos se hagan con
respecto a un sistema inercial, es decir, con respecto a un observador
que no esté sometido a ninguna aceleración, que no esté sometido
a ninguna fuerza resultante.
Si no es así, las ecuaciones dejan de ser válidas (la única
forma de hacer que entonces las ecuaciones todavía funcionen es
introduciendo fuerzas ficticias como la fuerza de inercia o la
centrífuga).
Por ello en las ecuaciones (3) y (5), el punto
de referencia O tiene que ser un punto no sometido a ninguna
aceleración.
Hay una excepción a esta regla: por la propia definición del
centro de masas, las ecuaciones (3) y (5)
siguen siendo válidas si O corresponde al centro de masas, aunque
éste sea una punto que lleve aceleración.
Volviendo a la ecuación
 ,
se siguen los mismos comentarios que para la ecuación
(1):
si
,
se siguen los mismos comentarios que para la ecuación
(1):
si
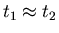 entonces el momento angular se conserva:
entonces el momento angular se conserva:
 .
O bien es válido en general
.
O bien es válido en general
 si,
independientemente de lo cerca o lejos que esté
si,
independientemente de lo cerca o lejos que esté  de
de  ,
se cumple
,
se cumple
 .
.
Aparte de todo esto, y para terminar, siempre se cumple que la
variación de la energía mecánica entre dos puntos es igual al
trabajo realizado por las fuerzas no conservativas, esto es, fuerzas
del tipo de rozamientos o donde entran motores que están emitiendo
calor a medida que hacen trabajo (es decir, todos los motores):
 |
(6) |
donde la energía cinética
 es la suma de la energía cinética de traslación del centro de
masa más la energía cinética de rotación, si la hay;
y la energía potencial
es la suma de la energía cinética de traslación del centro de
masa más la energía cinética de rotación, si la hay;
y la energía potencial
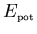 es la suma de la
energía potencial gravitatoria más la electrostática (debida a
una carga eléctrica dentro de una campo eléctrico) y más la
elástica (debida al estiramiento elástico de un muelle).
es la suma de la
energía potencial gravitatoria más la electrostática (debida a
una carga eléctrica dentro de una campo eléctrico) y más la
elástica (debida al estiramiento elástico de un muelle).
Ejemplo: Aplicación de todo lo anterior a un problema de la
Olimpiada Internacional de Física celebrada en 1991 en La Habana.
Una bola de masa uniforme m y radio R está inicialmente
girando en torno a su centro de masas con una velocidad angular constante
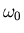 ; el centro de masas está quieto quedando el punto más
bajo de la bola a una altura
; el centro de masas está quieto quedando el punto más
bajo de la bola a una altura  sobre el suelo (ver la figura).
sobre el suelo (ver la figura).
A continuación se deja caer la bola, rebota en el suelo y
sube hasta una altura 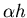 .
Se supone que la bola no se deforma en el choque (esto es, que es un
cuerpo rígido), y se da como dato del problema que el coeficiente
de rozamiento dinámico entre la bola y el suelo es
.
Se supone que la bola no se deforma en el choque (esto es, que es un
cuerpo rígido), y se da como dato del problema que el coeficiente
de rozamiento dinámico entre la bola y el suelo es  .
El momento de inercia de una bola con respecto a un eje que pasa por
el centro de masa es
.
El momento de inercia de una bola con respecto a un eje que pasa por
el centro de masa es
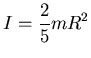 .
Puesto que la dirección en la que sale la bola después del choque
no es la misma que en la que ha caído, y ya que hay fuerzas
externas a la bola durante todo el choque, es claro que este choque ha
durado un intervalo de tiempo que no es despreciable.
.
Puesto que la dirección en la que sale la bola después del choque
no es la misma que en la que ha caído, y ya que hay fuerzas
externas a la bola durante todo el choque, es claro que este choque ha
durado un intervalo de tiempo que no es despreciable.
Se pide lo siguiente:
- Suponiendo que la bola roza deslizando durante todo el tiempo
que dura la interacción con el suelo, calcular el valor del ángulo
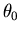 .
Para este caso, por tanto, no hay ninguna elación directa entre la
velocidad de rotación de la bola y la velocidad de desplazamiento de
su centro de masas.
.
Para este caso, por tanto, no hay ninguna elación directa entre la
velocidad de rotación de la bola y la velocidad de desplazamiento de
su centro de masas.
- Suponiendo ahora que el rozamiento deslizando acaba antes de
que empiece a elevarse la bola del suelo, volver a calcular
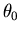 .
En este caso, cuando la bola justo antes de dejar el suelo sí que
está rodando sin deslizar y por lo tanto sí que hay una
relación directa entre la velocidad de rotación después
del choque y la velocidad de desplazamiento horizontal del centro de masas.
.
En este caso, cuando la bola justo antes de dejar el suelo sí que
está rodando sin deslizar y por lo tanto sí que hay una
relación directa entre la velocidad de rotación después
del choque y la velocidad de desplazamiento horizontal del centro de masas.
Solución:
Mientras cae todos los puntos de la bola llevan aceleración y por
tanto, los cálculos que hagamos sobre momentos angulares los
referiremos al centro de masas.
Puesto que durante la caída la única fuerza que actúa sobre la
bola es su peso, y esta fuerza no tiene momento respecto del centro de
masas (ya que está aplicada justamente en el centro de masas),
entonces de acuerdo con (3) se cumple
 |
(7) |
o lo que es lo mismo, la velocidad angular permanece constante en
módulo y sentido durante toda la caída (el momento de inercia
I no cambia al ser una bola rígida).
Para saber con qué velocidad llega el centro de masas al suelo justo
antes del choque emplearemos la conservación de la energía
mecánica:
de donde se obtiene
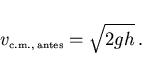 |
(8) |
Durante el intervalo de tiempo  que dura la interacción
con el suelo, la fuerza vertical de reacción del suelo (=la normal)
hace que la componente vertical de la velocidad del c.m. varíe de
acuerdo con la ecuación (1)
que dura la interacción
con el suelo, la fuerza vertical de reacción del suelo (=la normal)
hace que la componente vertical de la velocidad del c.m. varíe de
acuerdo con la ecuación (1)
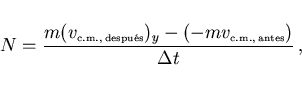 |
(9) |
mientras que la fuerza de rozamiento cambia la velocidad horizontal
del centro de masas (la bola ``empuja'' al suelo hacia atrás y el
suelo reponde ``empujando'' a la bola hacia adelante)
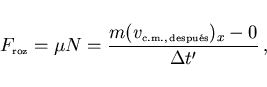 |
(10) |
siendo 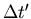 el tiempo que dura este rozamiento dinámico
(=deslizante).
En general
el tiempo que dura este rozamiento dinámico
(=deslizante).
En general 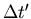 no tiene por qué ser igual al tiempo
no tiene por qué ser igual al tiempo
 que dura la interacción con el suelo: sencillamente, la
velocidad inicial de rotación de la bola podía haber sido tan
baja que al poco de empezar la interacción con el suelo, el punto de
contacto de la bola con el suelo (punto que lleva una velocidad hacia
adelante igual a
que dura la interacción con el suelo: sencillamente, la
velocidad inicial de rotación de la bola podía haber sido tan
baja que al poco de empezar la interacción con el suelo, el punto de
contacto de la bola con el suelo (punto que lleva una velocidad hacia
adelante igual a
 más una velocidad
hacia atrás debida a la rotación) llegara a tener una velocidad
cero, y en este caso empezamos a tener una rodadura sin deslizamiento.
más una velocidad
hacia atrás debida a la rotación) llegara a tener una velocidad
cero, y en este caso empezamos a tener una rodadura sin deslizamiento.
De las fuerzas que actúan sobre la bola durante el choque sólo la
fuerza de rozamiento tiene momento con respecto al centro de masas (la
fuerza normal apunta hacia c.m. y por tanto su momento es cero): este
momento vale
 y va en sentido contrario a la
velocidad angular (recordar que
y va en sentido contrario a la
velocidad angular (recordar que
 apunta hacia
adelante), por lo que a partir de (3) obtenemos
apunta hacia
adelante), por lo que a partir de (3) obtenemos
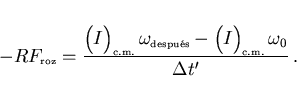 |
(11) |
Por último, nos queda relacionar la velocidad de desplazamiento del
centro de masas justo después del choque con la altura 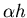 que alcanza la bola.
Esto se hace de la misma forma que para el resultado (8):
durante la subida, la única fuerza que actúa sobre la bola es su
peso, fuerza que no tiene momento respecto del c.m. (luego la
velocidad angular se conserva durante la subida) y que al actuar
sólo en la dirección vertical sólo modifica la componente
vertical de la velocidad del centro de masas:
que alcanza la bola.
Esto se hace de la misma forma que para el resultado (8):
durante la subida, la única fuerza que actúa sobre la bola es su
peso, fuerza que no tiene momento respecto del c.m. (luego la
velocidad angular se conserva durante la subida) y que al actuar
sólo en la dirección vertical sólo modifica la componente
vertical de la velocidad del centro de masas:
y por lo tanto
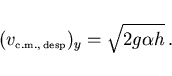 |
(12) |
Ahora ya sólo obtener
 .
.
- Para el primer caso en que durante todo el tiempo
 de
interacción de la bola con el suelo el rozamiento ha sido
deslizando y por tanto
de
interacción de la bola con el suelo el rozamiento ha sido
deslizando y por tanto
 , combinando resultados
(10) y (9) con (12) obtenemos
, combinando resultados
(10) y (9) con (12) obtenemos
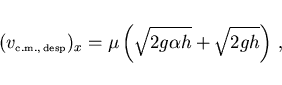 |
(13) |
y así
 |
(14) |
Si además queremos calcular
 ,
basta con combinar (11) y (10) con
(13)
,
basta con combinar (11) y (10) con
(13)
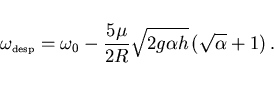 |
(15) |
- Para el segundo caso
 y por lo tanto no podemos
operar como en (13) y de la ecuación (9) no
podemos despejar
y por lo tanto no podemos
operar como en (13) y de la ecuación (9) no
podemos despejar  .
Sin embargo sí sabemos que en el momento en que la bola despega del suelo
ésta está rodando sin deslizar, y por definición de rodadura, la
velocidad de giro en torno al centro masas,
.
Sin embargo sí sabemos que en el momento en que la bola despega del suelo
ésta está rodando sin deslizar, y por definición de rodadura, la
velocidad de giro en torno al centro masas,
 , y
la velocidad de desplazamiento horizontalmente sobre el suelo del
centro de masas,
, y
la velocidad de desplazamiento horizontalmente sobre el suelo del
centro de masas,
 , están
relacionadas entre sí mediante la ecuación
, están
relacionadas entre sí mediante la ecuación
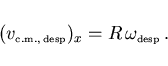 |
(16) |
A partir de las ecuaciones (11) y (10)
 |
(17) |
y puesto que la solución
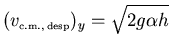 se sigue
cumpliendo ya que se obtuvo a partir de la conservación de la
energía después del choque, obtenemos entonces
se sigue
cumpliendo ya que se obtuvo a partir de la conservación de la
energía después del choque, obtenemos entonces
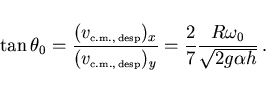 |
(18) |
TRUCOS PARA LOS PROBLEMAS EXPERIMENTALES
Antes de empezar, un par de aproximaciones útiles para los problemas
tanto teóricos como experimentales: cuando  se cumple que
se cumple que
siendo este resultado válido para cualquier k.
Si x está medido en radianes, entonces se cumple que
cuando x es pequeño en comparación con 1 radián.
Ahora los trucos para los problemas experimentales: supongamos que
tenemos una variable F en función de otra variable z,
siendo la dependencia entre ambas de la forma
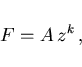 |
(19) |
con A y k dos constantes desconocidas.
Además nos dan una tabla de datos con los valores de z y los
correspondientes valores de F, y nos piden hallar A y
k.
Esto se hace de la siguiente forma: tomando el logaritmo (decimal o
neperiano, da igual) de la ecuación (19) obtenemos
 |
(20) |
Si ahora representamos en papel milimetrado logF en el eje
vertical y logz en el eje vertical, puesto que logF es
directamente proporcional a logz (como se ve en la ecuación
(20)), lo que obtenemos es una recta de pendiente
k (es decir, midiendo el ángulo que forma la recta con el eje
horizontal, su tangente es igual a k) y de ordenada en el origen
logA (es decir, midiendo sobre la gráfica a qué altura corta
la recta al eje vertial para logz=0, obtendremos logA).
Suponiendo que el exponente k de la ecuación (19)
ya lo conociéramos de antemano, otra forma de hallar la constante
A es la siguiente: representamos en el eje vertical el valor de
F y en el eje horizontal el valor de 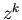 .
Puesto que F es directamente proporcional a
.
Puesto que F es directamente proporcional a 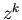 , la gráfica
resultante vuelve a ser una recta, que pasa esta vez por el origen y
que tiene una pendiente que es precisamente A.
Este método puede aplicarse a un caso un poco más general
, la gráfica
resultante vuelve a ser una recta, que pasa esta vez por el origen y
que tiene una pendiente que es precisamente A.
Este método puede aplicarse a un caso un poco más general
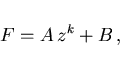 |
(21) |
con A y B constantes desconocidas pero con el exponente
k conocido.
Representando F en el eje vertical y 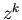 en el eje horizontal,
volvemos a obtener una recta de pendiente A y ordenada en el
origen igual a B (es decir, la altura donde la recta corta al
eje vertical para z=0 nos da directamente B).
Date cuenta que si k lo desconociéramos, en la ecuación
(21) ya no podríamos aplicar el procedimiento de tomar
logaritmos, ya que el logaritmo de una suma no se puede separar en
términos más sencillos.
en el eje horizontal,
volvemos a obtener una recta de pendiente A y ordenada en el
origen igual a B (es decir, la altura donde la recta corta al
eje vertical para z=0 nos da directamente B).
Date cuenta que si k lo desconociéramos, en la ecuación
(21) ya no podríamos aplicar el procedimiento de tomar
logaritmos, ya que el logaritmo de una suma no se puede separar en
términos más sencillos.
Ejemplo: como ya habrás visto, en todos los casos se trata de
ingeniárselas y buscar qué es lo que hay que representar en cada
eje para que la gráfica resultante salga una recta, de la que
así podemos leer fácilmente la pendiente y la ordenada en el origen.
Supongamos que nos dieran los datos de F y de z y que
además nos dijeran que estos datos responden a la ecuación
y ahora nos pidieran que con esos datos hallármos A y B.
La forma de resolverlo es bien fácil: si escribimos
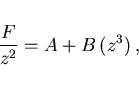 |
(22) |
y representamos en el eje vertical
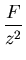 y en el eje horizontal
y en el eje horizontal
 , entonces la gráfica será una
recta, de acuerdo con la ecuación (22).
Y la pendiente de tal recta será B, mientras que la ordenada
en el origen será A.
, entonces la gráfica será una
recta, de acuerdo con la ecuación (22).
Y la pendiente de tal recta será B, mientras que la ordenada
en el origen será A.



Next: Fase Local de La Rioja 2002
Up: Olimpiadas de Física
José Luis Marqués 15.02.02
![]() y
y ![]() muy poco separados entre sí, se
cumple que
muy poco separados entre sí, se
cumple que
![]() (por
ejemplo, consideramos el instante justo antes y
justo después de un choque que no dura prácticamente nada de
tiempo), entonces se cumple
(por
ejemplo, consideramos el instante justo antes y
justo después de un choque que no dura prácticamente nada de
tiempo), entonces se cumple
![]() , es decir,
el momento lineal del centro de masas se conserva.
Evidentemente, el momento lineal también se conserva
independientemente de lo cercano que esté
, es decir,
el momento lineal del centro de masas se conserva.
Evidentemente, el momento lineal también se conserva
independientemente de lo cercano que esté ![]() de
de ![]() si
si
![]() .
.
![]() y
y ![]() muy poco separados entre sí
muy poco separados entre sí
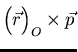 .
En el caso de un sistema de partículas, el momento angular es la
suma de los momentos angulares de cada una de las partículas; y si
además se cumple que el cuerpo es rígido (=no deformable)
entonces se puede demostrar que
.
En el caso de un sistema de partículas, el momento angular es la
suma de los momentos angulares de cada una de las partículas; y si
además se cumple que el cuerpo es rígido (=no deformable)
entonces se puede demostrar que
![]() se puede escribir también de la siguiente forma
se puede escribir también de la siguiente forma

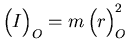 ; y por ejemplo para un
un disco macizo de masa
; y por ejemplo para un
un disco macizo de masa 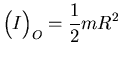 .
.
![]() de una fuerza
de una fuerza
![]() respecto a un punto O está definido por el producto
vectorial
respecto a un punto O está definido por el producto
vectorial
![]() ,
se siguen los mismos comentarios que para la ecuación
(1):
si
,
se siguen los mismos comentarios que para la ecuación
(1):
si
![]() entonces el momento angular se conserva:
entonces el momento angular se conserva:
![]() .
O bien es válido en general
.
O bien es válido en general
![]() si,
independientemente de lo cerca o lejos que esté
si,
independientemente de lo cerca o lejos que esté ![]() de
de ![]() ,
se cumple
,
se cumple
![]() .
.
![]() ; el centro de masas está quieto quedando el punto más
bajo de la bola a una altura
; el centro de masas está quieto quedando el punto más
bajo de la bola a una altura ![]() sobre el suelo (ver la figura).
sobre el suelo (ver la figura).
![]() .
Se supone que la bola no se deforma en el choque (esto es, que es un
cuerpo rígido), y se da como dato del problema que el coeficiente
de rozamiento dinámico entre la bola y el suelo es
.
Se supone que la bola no se deforma en el choque (esto es, que es un
cuerpo rígido), y se da como dato del problema que el coeficiente
de rozamiento dinámico entre la bola y el suelo es ![]() .
El momento de inercia de una bola con respecto a un eje que pasa por
el centro de masa es
.
El momento de inercia de una bola con respecto a un eje que pasa por
el centro de masa es
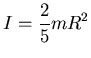 .
Puesto que la dirección en la que sale la bola después del choque
no es la misma que en la que ha caído, y ya que hay fuerzas
externas a la bola durante todo el choque, es claro que este choque ha
durado un intervalo de tiempo que no es despreciable.
.
Puesto que la dirección en la que sale la bola después del choque
no es la misma que en la que ha caído, y ya que hay fuerzas
externas a la bola durante todo el choque, es claro que este choque ha
durado un intervalo de tiempo que no es despreciable.
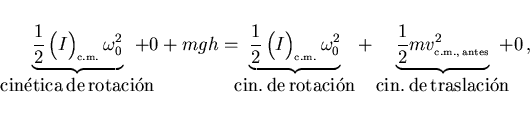
![]() que dura la interacción
con el suelo, la fuerza vertical de reacción del suelo (=la normal)
hace que la componente vertical de la velocidad del c.m. varíe de
acuerdo con la ecuación (1)
que dura la interacción
con el suelo, la fuerza vertical de reacción del suelo (=la normal)
hace que la componente vertical de la velocidad del c.m. varíe de
acuerdo con la ecuación (1)
![]() y va en sentido contrario a la
velocidad angular (recordar que
y va en sentido contrario a la
velocidad angular (recordar que
![]() apunta hacia
adelante), por lo que a partir de (3) obtenemos
apunta hacia
adelante), por lo que a partir de (3) obtenemos


 .
.
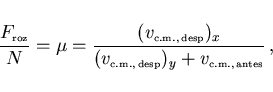
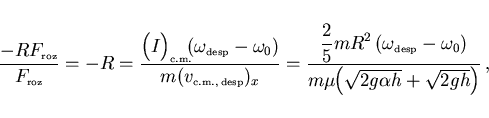
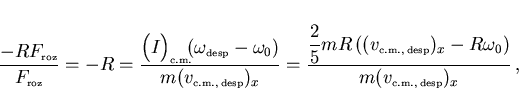
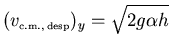 se sigue
cumpliendo ya que se obtuvo a partir de la conservación de la
energía después del choque, obtenemos entonces
se sigue
cumpliendo ya que se obtuvo a partir de la conservación de la
energía después del choque, obtenemos entonces
![]() se cumple que
se cumple que
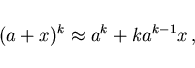

![]() .
Puesto que F es directamente proporcional a
.
Puesto que F es directamente proporcional a ![]() , la gráfica
resultante vuelve a ser una recta, que pasa esta vez por el origen y
que tiene una pendiente que es precisamente A.
Este método puede aplicarse a un caso un poco más general
, la gráfica
resultante vuelve a ser una recta, que pasa esta vez por el origen y
que tiene una pendiente que es precisamente A.
Este método puede aplicarse a un caso un poco más general
