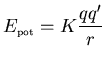 para dos cargas q y
q' separadas en el vacío una distancia r,
con K una constante igual a
para dos cargas q y
q' separadas en el vacío una distancia r,
con K una constante igual a
Puesto que el campo electrostático es conservativo, se puede definir
una energía potencial, que es igual a
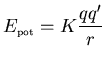 para dos cargas q y
q' separadas en el vacío una distancia r,
con K una constante igual a
para dos cargas q y
q' separadas en el vacío una distancia r,
con K una constante igual a
![]() (nota que se
trata de una forma de energía potencial muy similar a la del
problema anterior, aunque ahora con cargas eléctricas en vez de masa).
Si suponemos que el rozamiento con el aire es despreciable, el
problema lo podemos resolver por conservación de la energía
mecánica (suma de energía cinética y de las energías
potenciales).
(nota que se
trata de una forma de energía potencial muy similar a la del
problema anterior, aunque ahora con cargas eléctricas en vez de masa).
Si suponemos que el rozamiento con el aire es despreciable, el
problema lo podemos resolver por conservación de la energía
mecánica (suma de energía cinética y de las energías
potenciales).
En la posición de partida, la carga Q que está arriba no
tiene nada de energía cinética (está quieta), tiene una
energía potencial gravitatoria igual a ![]() (con
(con
![]() ) y una energía potencial electrostática
igual a
) y una energía potencial electrostática
igual a
![]() (suponemos que las bolitas son
prácticamente puntuales, de tal forma que
(suponemos que las bolitas son
prácticamente puntuales, de tal forma que ![]() es la distancia
que las separa inicialmente).
es la distancia
que las separa inicialmente).
Soltamos la bola, va cayendo y acelerándose por acción de la
gravedad pero a medida que se acerca a la otra bolita es repelida por
esta.
En el punto más cercano a la bolita que está en el suelo,
parándose a una distancia
![]() de ella, la
energía mecánica es la misma que al inicio:
de ella, la
energía mecánica es la misma que al inicio:
Si ahora consideramos un punto cualquiera de la trayectoria de la
bolita, cuando está a una distancia h de la bolita inferior y
lleva una velocidad v, tenemos entonces que la misma ecuación
(9) se aplica aquí
![]() Si ahora queremos saber para qué valor h' de la altura la
velocidad v es máxima, argumentamos de la siguiente forma:
para que la velocidad sea máxima (para que la energía
cinética sea máxima), la energía potencial total
Si ahora queremos saber para qué valor h' de la altura la
velocidad v es máxima, argumentamos de la siguiente forma:
para que la velocidad sea máxima (para que la energía
cinética sea máxima), la energía potencial total
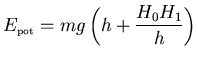 ha de ser
mínima ya que la suma de las dos, la energía mecánica, es
constante.
Luego hay que buscar el valor de h que hace que la derivada de
la energía potencial con respecto a h sea cero:
ha de ser
mínima ya que la suma de las dos, la energía mecánica, es
constante.
Luego hay que buscar el valor de h que hace que la derivada de
la energía potencial con respecto a h sea cero:
![]() La correspondiente velocidad máxima se obtiene de sustituir
h' en (12)
La correspondiente velocidad máxima se obtiene de sustituir
h' en (12)
![\begin{displaymath}
mg(H_0+H_1)=\frac m2 v_{\scriptscriptstyle \rm max}^2+mg\lef...
...{\scriptscriptstyle \rm max}^2}{2g}+2\sqrt{H_0 H_1}\right]\, ,
\end{displaymath}](img46.png)
![]() Ahora tenemos que calcular en qué punto de toda la
trayectoria la aceleración (o lo que es lo mismo, la fuerza) es la mayor.
Sobre la bolita que cae actúan dos fuerzas: la del peso (que es
constante e igual a mg) y la de la repulsión entre las dos
bolitas.
Esta repulsión es la mayor posible en el punto en el que están
más cerca, luego en este punto es donde la aceleración de frenado
es la mayor; y es la menor posible en el punto en que están más
alejadas (al inicio del experimento).
Puesto que la aceleración total es la resta de la aceleración de la
gravedad g menos esta desaceleración por la repulsión entre
las dos cargas eléctricas, entonces
Ahora tenemos que calcular en qué punto de toda la
trayectoria la aceleración (o lo que es lo mismo, la fuerza) es la mayor.
Sobre la bolita que cae actúan dos fuerzas: la del peso (que es
constante e igual a mg) y la de la repulsión entre las dos
bolitas.
Esta repulsión es la mayor posible en el punto en el que están
más cerca, luego en este punto es donde la aceleración de frenado
es la mayor; y es la menor posible en el punto en que están más
alejadas (al inicio del experimento).
Puesto que la aceleración total es la resta de la aceleración de la
gravedad g menos esta desaceleración por la repulsión entre
las dos cargas eléctricas, entonces
![]() Sabiendo el valor de la masa m, el valor de Q se
deduce inmediatamente de (10):
Sabiendo el valor de la masa m, el valor de Q se
deduce inmediatamente de (10):