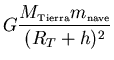 , siendo
, siendo
![]() La fuerza externa que actúa sobre la nave es sólo la de la
atracción gravitatoria terrestre, que según la Ley de Newton viene
dada por
La fuerza externa que actúa sobre la nave es sólo la de la
atracción gravitatoria terrestre, que según la Ley de Newton viene
dada por
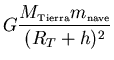 , siendo
, siendo ![]() la distancia entre la nave y
el centro de la Tierra.
La dirección de esta fuerza es central, esto es, apuntando hacia el
centro de la Tierra, y por tanto es perpendicular a la trayectoria
circular de la nave: por ello, esta fuerza no hace trabajo y no
modifica la energía cinética (el módulo de la velocidad) de la nave.
la distancia entre la nave y
el centro de la Tierra.
La dirección de esta fuerza es central, esto es, apuntando hacia el
centro de la Tierra, y por tanto es perpendicular a la trayectoria
circular de la nave: por ello, esta fuerza no hace trabajo y no
modifica la energía cinética (el módulo de la velocidad) de la nave.
Tal fuerza es igual a la masa de la nave multiplicada por su
aceleración: puesto que la fuerza es perpendicular a la trayectoria,
no hay aceleración tangencial (tangente a la trayectoria) sino
sólamente existe la aceleración normal (perpendicular a la
trayectoria):
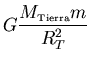 , de donde despejamos que
, de donde despejamos que
![]() Una vez la nave ya ha empezado la trayectoria curvada de
aproximación, la única fuerza externa que actúa sobre la nave
vuelve a ser la gravitatoria, que como ya sabes es una que apunta al
centro de la Tierra.
Tal fuerza no cambia el momento angular
Una vez la nave ya ha empezado la trayectoria curvada de
aproximación, la única fuerza externa que actúa sobre la nave
vuelve a ser la gravitatoria, que como ya sabes es una que apunta al
centro de la Tierra.
Tal fuerza no cambia el momento angular ![]() de la nave
(Ley de Kepler), momento que medido desde el centro de la Tierra es
de la nave
(Ley de Kepler), momento que medido desde el centro de la Tierra es
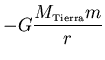 (el signo menos indica que
la masa m es más estable, tiene menos energía potencial a
una distancia finita de la Tierra que a una distancia infinita); y por
lo tanto
(el signo menos indica que
la masa m es más estable, tiene menos energía potencial a
una distancia finita de la Tierra que a una distancia infinita); y por
lo tanto
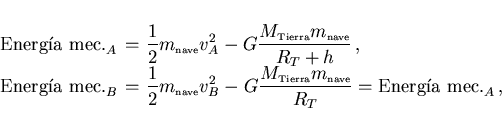
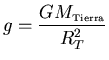 , obtenemos
, obtenemos
![]() En teoría, y ya que conocemos
En teoría, y ya que conocemos ![]() , podríamos resolver
esta cuestión como en (4), utilizando la conservación del
momento angular al no tener más que una fuerza exterior que es central.
El único problema es que para calcular el momento angular (medido
desde el centro de la Tierra) de la nave en el punto C
necesitamos conocer el ángulo que forma la velocidad de la nave con
respecto al vector de posición: recuerda que el momento angular se
define a traés de un producto vectorial
, podríamos resolver
esta cuestión como en (4), utilizando la conservación del
momento angular al no tener más que una fuerza exterior que es central.
El único problema es que para calcular el momento angular (medido
desde el centro de la Tierra) de la nave en el punto C
necesitamos conocer el ángulo que forma la velocidad de la nave con
respecto al vector de posición: recuerda que el momento angular se
define a traés de un producto vectorial
![]() ; este problema no lo tenía mos
en el caso anterior ya que en los puntos A y B el vector
de posición y la velocidad eran perpendiculares entre sí.
; este problema no lo tenía mos
en el caso anterior ya que en los puntos A y B el vector
de posición y la velocidad eran perpendiculares entre sí.
Luego el momento angular no nos sirve.
Sin embargo, como nos dicen que, en el caso que estamos estudiando
ahora, hasta este punto C la nave no ha rozado todavía con
la atmósfera, entonces la energía mecánica de la nave
se conserva
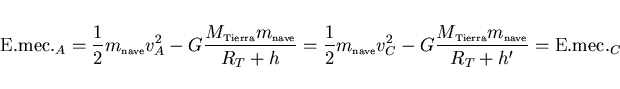
![]() Suponiendo que la reducción de energía cinética de la
nave sólo es debida al rozamiento con la atmósfera (despreciamos
el trabajo de frenado de los cohetes), entonces el trabajo hecho por
tal rozamiento es igual a la variación de energía mecánica
(que por lo tanto ya no se conserva) entre los puntos C y el
punto de aterrizaje (donde la nave ya no lleva velocidad):
Suponiendo que la reducción de energía cinética de la
nave sólo es debida al rozamiento con la atmósfera (despreciamos
el trabajo de frenado de los cohetes), entonces el trabajo hecho por
tal rozamiento es igual a la variación de energía mecánica
(que por lo tanto ya no se conserva) entre los puntos C y el
punto de aterrizaje (donde la nave ya no lleva velocidad):
![\begin{displaymath}
W_{\scriptscriptstyle \rm roz}=\left[\frac 12 m_{\scriptscri...
...le \rm Tierra}m_{\scriptscriptstyle \rm nave}}{R_T}\right]\, ,
\end{displaymath}](img28.png)