
Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
Durante todo el problema vamos a suponer que el hilo no se estira ni
tiene masa, y que la polea por donde pasa el hilo tampoco tiene masa.
Con esto podemos asegurar que la tensión en el hilo es la misma a lo
largo de todo el hilo, y que la aceleración con la que cae la pesa
es la misma que la aceleración con la que se mueve el carrito hacia
la derecha.
Aplicando la segunda ley de Newton a cada una de las masas de la
figura se despeja que la aceleración a viene dada por
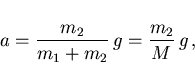 |
(11) |
siendo 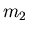 la masa del carrito (que en cada nuevo intento vamos a ir
variando), M la masa total del carrito+pesa (que es constante e
igual a 0.15kg), y g la aceleración de la gravedad que
queremos obtener.
Puesto que la aceleración (11) no varía con el tiempo, el
movimiento del carrito es uniformemente acelerado: como el carrito
parte del reposo siempre, el espacio recorrido d está
relacionado con la aceleración por
la masa del carrito (que en cada nuevo intento vamos a ir
variando), M la masa total del carrito+pesa (que es constante e
igual a 0.15kg), y g la aceleración de la gravedad que
queremos obtener.
Puesto que la aceleración (11) no varía con el tiempo, el
movimiento del carrito es uniformemente acelerado: como el carrito
parte del reposo siempre, el espacio recorrido d está
relacionado con la aceleración por
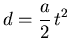 , siendo t
el tiempo en recorrer este espacio.
O sea,
, siendo t
el tiempo en recorrer este espacio.
O sea,
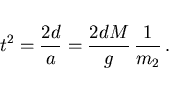 |
(12) |
Si representáramos el tiempo t frente a la masa del carrito
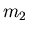 obtendríamos una curva similar a una hipérbola, de
la que no podemos sacar mucha información.
Sin embargo, con un poco de astucia (ver
trucos) y
fijándonos bien en la ecuación (12) vemos que
obtendríamos una curva similar a una hipérbola, de
la que no podemos sacar mucha información.
Sin embargo, con un poco de astucia (ver
trucos) y
fijándonos bien en la ecuación (12) vemos que 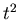 es
directamente proporcional a
es
directamente proporcional a 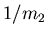 , o lo que es lo mismo, si
representamos en el eje vertical
, o lo que es lo mismo, si
representamos en el eje vertical 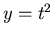 y en el eje horizontal
y en el eje horizontal 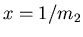 tenemos
tenemos
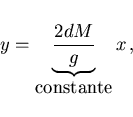
que es la ecuación de una recta de pendiente igual a 2dM/g
y que pasa por el origen de coordenadas.
Tras representar esta recta con los datos de la tabla, obtenemos su
pendiente: por ejemplo, midiendo el ángulo que forma la recta con el
eje horizontal y calculando su tangente trigonométrica, o bien
midiendo la altura de un punto cualquiera de la recta y dividiendo
esta altura por la abcisa correspondiente
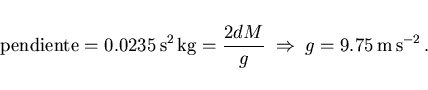 |
(13) |
Otra forma (menos elegante) de obtener g es despejar su valor a
partir del resultado (12) sustituyendo para cada pareja de
datos de la tabla; y luego calcular el valor medio de todos los
valores de g obtenidos.

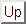

Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
José Luis Marqués 15.02.02
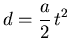 , siendo t
el tiempo en recorrer este espacio.
O sea,
, siendo t
el tiempo en recorrer este espacio.
O sea,