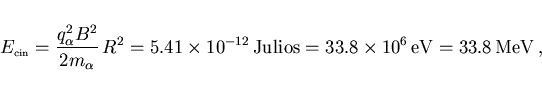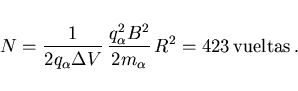Teniendo en cuenta el producto vectorial que entra en la definición de
la fuerza de Lorentz
![]() , la fuerza debida a
un campo magnético B sobre una partícula de carga q
y velocidad v tiene la dirección representada en la siguiente
figura, respectivamente, para una partícula cargada negativamente
(izquierda) o positivamente (derecha).
, la fuerza debida a
un campo magnético B sobre una partícula de carga q
y velocidad v tiene la dirección representada en la siguiente
figura, respectivamente, para una partícula cargada negativamente
(izquierda) o positivamente (derecha).
Como se ve, la fuerza de Lorentz ``tira'' de la partícula en
dirección perpendicular a la velocidad ![]() , luego una
fracción de tiempo
, luego una
fracción de tiempo ![]() muy pequeña después, la velocidad
será (vista desde arriba) como en el siguiente dibujo:
muy pequeña después, la velocidad
será (vista desde arriba) como en el siguiente dibujo:
Sin embargo, esta fuerza no modifica el módula de la velocidad ya
que la fuerza no hace ningún trabajo por ser perpendicular a la
velocidad
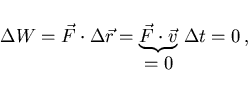
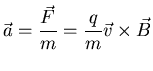 , responsable de este cambio de
dirección de la velocidad, apunta en dirección normal o centrípeta
, responsable de este cambio de
dirección de la velocidad, apunta en dirección normal o centrípeta
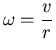 la velocidad angular (medida en rad/s), también llamada frecuencia
de ciclotrón.
El tiempo que tarda en dar una vuelta (o sea,
la velocidad angular (medida en rad/s), también llamada frecuencia
de ciclotrón.
El tiempo que tarda en dar una vuelta (o sea,
Notar que
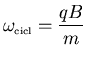 (7) es
independiente del radio r de la trayectoria, lo que permite el
montaje experimental descrito en cursiva en el enunciado del problema.
Vamos a repasarlo un poco.
Supongamos que el campo eléctrico que acelera las partículas al
pasar entre las dos ``des'' (en el interior de las ``des'' el campo
eléctrico no puede entrar) fuera constante con el tiempo, tal y como está
representado en la figura.
En el punto P1 la partícula sería acelerada tal que su
energía cinética se vería incrementada en una cantidad igual
a
(7) es
independiente del radio r de la trayectoria, lo que permite el
montaje experimental descrito en cursiva en el enunciado del problema.
Vamos a repasarlo un poco.
Supongamos que el campo eléctrico que acelera las partículas al
pasar entre las dos ``des'' (en el interior de las ``des'' el campo
eléctrico no puede entrar) fuera constante con el tiempo, tal y como está
representado en la figura.
En el punto P1 la partícula sería acelerada tal que su
energía cinética se vería incrementada en una cantidad igual
a ![]() , que es el trabajo hecho por el campo eléctrico,
siendo
, que es el trabajo hecho por el campo eléctrico,
siendo ![]() la diferencia de potencial entre las dos ``des''.
la diferencia de potencial entre las dos ``des''.
Pero con un campo eléctrico constante en el tiempo, en P2 la partícula sería frenada, perdiendo justo la misma cantidad de energía cinética que había ganado en P1. Por lo tanto, el campo eléctrico tiene que cambiar de sentido (es decir, oscilar) con el mismo periodo (8) con el que la partícula está girando. Así aseguramos que cuando la partícula llegue a P2 la dirección del campo eléctrico ya ha cambiado y sigue acelerando a la partícula.
Para el caso de una partícula alfa acelerada en un campo
magnético B=1.4Teslas, este periodo y frecuencia se
obtienen inmediatamente de (8)