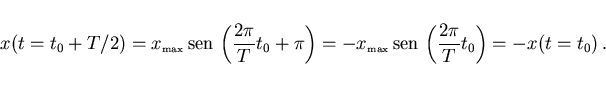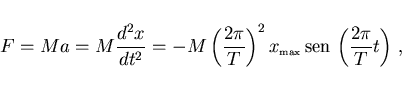Problema 1

Lo primero es darse cuenta que la fuerza que hay que hacer para desplazar el punch de su posición de equilibrio es directamente proporcional a este desplazamiento. O sea, el punch funciona como un muelle elástico de constante recuperadora

$$K=\frac{50 {\rm N}}{0.10 {\rm m}}\approx \frac{100 {\rm N... ...\frac{150 {\rm N}}{0.301 {\rm m}} \approx 500 {\rm N/m} ,$$

siendo por tanto la fuerza con la que se opone a un desplazamiento x igual a

$$F=-Kx .$$ (1)

Y así la energía potencial almacenada por el punch cuando se separa una distancia x de su posición de equilibrio es ${\displaystyle E_{\scriptscriptstyle \rm pot}=\frac 12Kx^2}$.

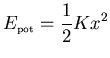El choque entre la bola de acero y la cabeza del punch no es elástico, es decir, no toda la energía cinética que lleva la bola justo antes de chocar es transferida al punch. Para que en un choque de una bola móvil contra otra que está en reposo se cumpliera que después del choque, la primera se quedara quieta y la segunda se moviera, y además toda la energía cinética de la primera pasara a la segunda, la masa de la primera tendría que ser igual a la masa de la segunda bola (por ejemplo, como sucede con las bolas de billar). En nuestro caso esto no se cumple ya que la masa del punch es mayor que la de la bola de acero que choca contra él. Y como vamos a ver, es el cociente entre estas dos masas lo que indica qué fracción de la energía cinética que llevaba la bola de acero justo antes del choque se la lleva el punch justo después.

En general en un choque la energía mecánica no se conserva; y en nuestro caso tampoco la energía cinética lo hace, ya que el choque ocurre a la misma altura y no hace falta tener en cuenta la variación de enegía potencial gravitatoria durante el choque. Sin embargo, el momento lineal del sistema sí que se conserva, siempre que comparemos la situación justo antes del choque con la situación justo después: ver repaso. Si $v_0$ es la velocidad de la bola justo antes del choque, entoces la velocidad de retroceso del punch justo después del choque viene dada por

$$\left. \begin{array}{lcl} \left(p_{\scriptscriptstyle \rm si... ...row v_{\scriptscriptstyle \rm retr}^2=\frac{m^2}{M^2}v_0^2 .$$ (2)

Con ello la energía cinética del sistema justo antes y justo después del choque están relacionadas por

$$% latex2html id marker 357\hspace{-1cm} \left. \begin{arra... ...yle \rm cin}\right)_{\scriptscriptstyle \rm justo\:antes}} .$$ (3)

Así sólo la fracción m/M=2/5=0.4 (un 40%) de la energía cinética que llevaba la bola justo antes del choque es transmitida al punch. El resto, un 60% se pierde en forma de calor y deformación del punch durante el choque, choque que es por tanto inelástico.

La energía mecánica (que es la suma de la energía cinética y de todas las energías potenciales) sí que se conserva, sin embargo, tanto durante el tramo en que la bola de acero cae desde su altura máxima hasta el choque, ${\displaystyle 0+mgh_0=\frac 12 mv_0^2+0}$, como después del choque durante el movimiento en que la energía cinética de partida se va almacenando en forma de energía potencial elástica hasta llegar al desplazamiento máximo ${x_{\scriptscriptstyle \rm max}=0.13 {\rm m}}$ (y suponiendo que la cabeza del punch no varía prácticamente de altura, para no necesitar considerar la energía potencial gravitatoria)

$$\frac 12 K x_{\scriptscriptstyle \rm max}^2 =\left(E_{\scrip... ...tscriptstyle \rm justo\:antes} =\left(\frac mM\right)mgh_0 ,$$ (4)

de donde obtenemos ${\displaystyle h_0=\frac{M}{m^2}\frac{Kx_{\scriptscriptstyle \rm max}^2}{2g}=53.8 {\rm cm}}$.

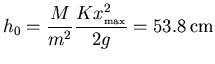Puesto que ya sabemos que opera como un muelle, el punch después del primer choque y hasta que retrocediendo vuelve a chocar con la bola, realiza un movimiento oscilatorio armónico simple. O lo que es lo mismo, su desplazamiento con el tiempo (contando el tiempo a partir del choque) viene dado por la ecuación

$$x(t)=x_{\scriptscriptstyle \rm max} {\rm sen} \left(\frac{2\pi}{T}t\right) ,$$ (5)

donde T/2 es el tiempo que tarda en hacer media oscilación, es decir, el tiempo en pasar de x a -x

$$x(t=t_0+T/2)=x_{\scriptscriptstyle \rm max} {\rm sen} \lef... ... max} {\rm sen} \left(\frac{2\pi}{T}t_0\right)=-x(t=t_0) .$$

Lo que tenemos que calcular para la última cuestión del problema es T/2: como ya sabemos de la ecuación (1), la fuerza viene dada por

$$F=-K x_{\scriptscriptstyle \rm max} {\rm sen} \left(\frac{2\pi}{T}t\right) ,$$

pero también sabemos por la segunda ley de Newton que esta fuerza es Ma

$$F=Ma=M\frac{d^2x}{dt^2}=-M\left(\frac{2\pi}{T}\right)^2 x_{\... ...iptstyle \rm max} {\rm sen} \left(\frac{2\pi}{T}t\right) ,$$

con lo que comparando ambas ecuaciones obtenemos que

$$\frac T2=\pi\sqrt{\frac MK}=0.31 {\rm segundos} .$$ (6)