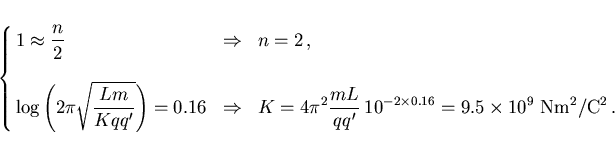

Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
Partimos de que la fuerza entre las cargas q y q' tiene
la forma
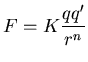 , con n número entero
desconocido y K una constante desconocida que tenemos que despejar.
Tal fuerza actúa en la dirección de la recta que une las dos
cargas.
Evidentemente en el montaje de la figura (en el que vamos a despreciar
desde el principio la atacción gravitatoria) tal fuerza no tiene una
dirección exactamente horizontal cuando el hilo de longitud L,
al que está unido la carga q, no está horizontal.
, con n número entero
desconocido y K una constante desconocida que tenemos que despejar.
Tal fuerza actúa en la dirección de la recta que une las dos
cargas.
Evidentemente en el montaje de la figura (en el que vamos a despreciar
desde el principio la atacción gravitatoria) tal fuerza no tiene una
dirección exactamente horizontal cuando el hilo de longitud L,
al que está unido la carga q, no está horizontal.
Sin embargo, suponiendo que la distancia r a la segunda carga
q' es mucho mayor que L, podemos aproximar la fuerza como
horizontal y además considerarla que es prácticamente constante.
Un caso similar ocurre con el péndulo simple dentro de un campo
gravitatorio: también al desplazar el péndulo de su posición
vertical la distancia al centro de La Tierra aumenta y la dirección
de la fuerza gravitatoria no es exactamente vertical, pero sin embargo
como la distancia al centro es mucho mayor que la longitud del
péndulo, podemos aproximar que la fuerza de atracción gravitatoria
sigue siendo vertical y con prácticamente el mismo valor que cuando
el péndulo colgaba verticalemnte.
Para el péndulo simple en el campo gravitatorio terrestre,
el periodo de su movimiento viene dado por
 si las oscilaciones son pequeñas.
En nuestro caso, la fuerza que actúa entre las dos cargas,
suponiendo que r sea mucho mayor que L, también la
podemos escribir como si se tratara de un campo gravitatorio
si las oscilaciones son pequeñas.
En nuestro caso, la fuerza que actúa entre las dos cargas,
suponiendo que r sea mucho mayor que L, también la
podemos escribir como si se tratara de un campo gravitatorio
donde la ``g'' ahora corresponde por tanto a
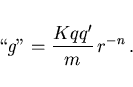 |
(16) |
Sustituyendo este resultado en el periodo de un péndulo simple en un
campo gravitatorio, obtenemos que el periodio en nuestro problema es
 |
(17) |
si las oscilaciones son pequeñas.
Ahora tenemos que despejar primeramente el número entero n que
aparece como exponente de r en la relación (17).
Puesto que
 es una constante,
tenemos que buscar un n entero tal que
es una constante,
tenemos que buscar un n entero tal que
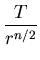 permanezca constante también.
Con los datos experimentales que tenemos, construimos la siguiente tabla:
permanezca constante también.
Con los datos experimentales que tenemos, construimos la siguiente tabla:
| |
r (en m) |
0.6 |
0.65 |
0.7 |
0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
| |
T (en s) |
0.84 |
0.94 |
1.00 |
1.08 |
1.12 |
1.22 |
1.30 |
1.38 |
1.43 |
| n=1 |
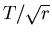 |
1.08 |
1.17 |
1.20 |
1.25 |
1.25 |
1.32 |
1.37 |
1.42 |
1.43 |
| n=2 |
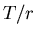 |
1.40 |
1.45 |
1.43 |
1.44 |
1.40 |
1.44 |
1.44 |
1.45 |
1.43 |
| n=3 |
 |
1.81 |
1.79 |
1.71 |
1.66 |
1.57 |
1.56 |
1.52 |
1.49 |
1.43 |
Por supuesto que no hace falta que hagas todos los cálculos de la tabla
anterior, basta con que tomes dos o tres valores: p.ej. los
correspondientes a r=0.6 m, r=0.8 m y r=1 m.
De los datos de esta tabla vemos que para n=1 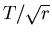 no
permanece constante al incrementar r.
Y otro tanto ocurre para n=3.
Sólo para n=2 se ve que T/r permanece aproximadamente
constante para cualquier valor de r: por lo tanto n=2.
Teniendo en cuenta (17) obtenemos
no
permanece constante al incrementar r.
Y otro tanto ocurre para n=3.
Sólo para n=2 se ve que T/r permanece aproximadamente
constante para cualquier valor de r: por lo tanto n=2.
Teniendo en cuenta (17) obtenemos
 ,
de donde, utilizando los datos al final del enunciado, se llega a
,
de donde, utilizando los datos al final del enunciado, se llega a
 |
(18) |
que es bastante parecido al valor real de
 .
.
Otra forma más elegante de resolver este problema sin necesidad de
elaborar la tabla anterior es utilizando el método que se explica en la
página dedicada a
trucos
para resolver problemas de olimpiada: como lo que queremos despejar es
un exponente desnocido, entonces representamos en el eje vertical el
logaritmo del periodo y en el eje horizontal el logaritmo de la
distancia, obteniendo la gráfica
de arriba.
De acuerdo con (17), tenemos por otra parte que
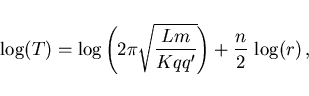 |
(19) |
luego los datos de la anterior gráfica estarán sobre una recta de
pendiente n/2 (de donde despejamos n) y tal recta, para un
valor de abcisa igual a 0, corta al eje vertical en un valor igual a
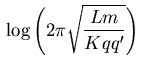 (de donde
despejamos K).
Esta pendiente se puede calcular tomando una pareja de puntos y viendo
cuál es la tangente trigonométrica de la inclinación de la
recta, que sale aproximadamente 1; y el término constante donde la
recta corta al eje vertical para un valor de la abcisa iguial a 0 es
aproximadamente 0.16
(de donde
despejamos K).
Esta pendiente se puede calcular tomando una pareja de puntos y viendo
cuál es la tangente trigonométrica de la inclinación de la
recta, que sale aproximadamente 1; y el término constante donde la
recta corta al eje vertical para un valor de la abcisa iguial a 0 es
aproximadamente 0.16
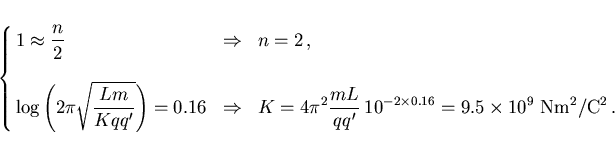 |
(20) |


Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
José Luis Marqués 15.02.02
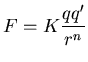 , con n número entero
desconocido y K una constante desconocida que tenemos que despejar.
Tal fuerza actúa en la dirección de la recta que une las dos
cargas.
Evidentemente en el montaje de la figura (en el que vamos a despreciar
desde el principio la atacción gravitatoria) tal fuerza no tiene una
dirección exactamente horizontal cuando el hilo de longitud L,
al que está unido la carga q, no está horizontal.
, con n número entero
desconocido y K una constante desconocida que tenemos que despejar.
Tal fuerza actúa en la dirección de la recta que une las dos
cargas.
Evidentemente en el montaje de la figura (en el que vamos a despreciar
desde el principio la atacción gravitatoria) tal fuerza no tiene una
dirección exactamente horizontal cuando el hilo de longitud L,
al que está unido la carga q, no está horizontal.
 si las oscilaciones son pequeñas.
En nuestro caso, la fuerza que actúa entre las dos cargas,
suponiendo que r sea mucho mayor que L, también la
podemos escribir como si se tratara de un campo gravitatorio
si las oscilaciones son pequeñas.
En nuestro caso, la fuerza que actúa entre las dos cargas,
suponiendo que r sea mucho mayor que L, también la
podemos escribir como si se tratara de un campo gravitatorio

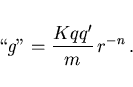

 es una constante,
tenemos que buscar un n entero tal que
es una constante,
tenemos que buscar un n entero tal que
 ,
de donde, utilizando los datos al final del enunciado, se llega a
,
de donde, utilizando los datos al final del enunciado, se llega a


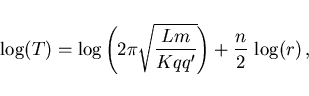
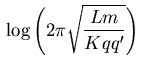 (de donde
despejamos K).
Esta pendiente se puede calcular tomando una pareja de puntos y viendo
cuál es la tangente trigonométrica de la inclinación de la
recta, que sale aproximadamente 1; y el término constante donde la
recta corta al eje vertical para un valor de la abcisa iguial a 0 es
aproximadamente 0.16
(de donde
despejamos K).
Esta pendiente se puede calcular tomando una pareja de puntos y viendo
cuál es la tangente trigonométrica de la inclinación de la
recta, que sale aproximadamente 1; y el término constante donde la
recta corta al eje vertical para un valor de la abcisa iguial a 0 es
aproximadamente 0.16