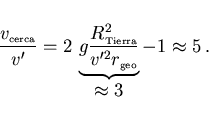Puesto que La Tierra da 1 vuelta (= ![]() radianes) en 1 día
(= 3600 x 24 segundos), su velocidad angular es
radianes) en 1 día
(= 3600 x 24 segundos), su velocidad angular es
Para la órbita se cumple que la fuerza que actúa sobre el
satélite, que es la gravitatoria
 ,
le produce al satélite exclusivamente una aceleración centrípeta:
,
le produce al satélite exclusivamente una aceleración centrípeta:
 ,
del resultado (7) se despeja el radio de la órbita geoestacionaria
,
del resultado (7) se despeja el radio de la órbita geoestacionaria
Recordemos que para un campo conservativo como el gravitatorio, a una
fuente puntual (para puntos fuera de La Tierra a ésta la podemos
considerar puntual) que crea un campo atractivo le corresponde una
energía potencial negativa:
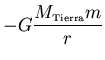 .
El signo menos es debido a que si para puntos infinitamente alejados
(
.
El signo menos es debido a que si para puntos infinitamente alejados
(![]() ), de forma que allá ya no se ``nota'' el campo
atractivo, entonces para puntos más próximos, donde una masa
está más ``sujeta'' por la atracción gravitatoria, la energía potencial tiene que ser menor que para puntos muy alejados: como
para el infinito la energía potencial es 0, para puntos más
próximos, la energía potencial (que es menor) tiene que ser
entonces negativa.
Para una masa m a una distancia r de una masa puntual M, y por tanto sometida a una energía potencial
), de forma que allá ya no se ``nota'' el campo
atractivo, entonces para puntos más próximos, donde una masa
está más ``sujeta'' por la atracción gravitatoria, la energía potencial tiene que ser menor que para puntos muy alejados: como
para el infinito la energía potencial es 0, para puntos más
próximos, la energía potencial (que es menor) tiene que ser
entonces negativa.
Para una masa m a una distancia r de una masa puntual M, y por tanto sometida a una energía potencial
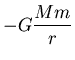 , se define la velocidad
, se define la velocidad
![]() como la
velocidad necesaria para escapar de tal campo gravitatorio atractivo
y llegar a un punto alejado infinitamente de cualquier masa (y por
tanto, un punto donde la energía potencial es 0) con una velocidad 0.
Por lo tanto, la energía mecánica (suma de energía
cinética y potencial) en este punto alejado infinitamente es 0, y
como la energía mecánica se conserva (suponemos que no hay
rozamientos en el espacio)
como la
velocidad necesaria para escapar de tal campo gravitatorio atractivo
y llegar a un punto alejado infinitamente de cualquier masa (y por
tanto, un punto donde la energía potencial es 0) con una velocidad 0.
Por lo tanto, la energía mecánica (suma de energía
cinética y potencial) en este punto alejado infinitamente es 0, y
como la energía mecánica se conserva (suponemos que no hay
rozamientos en el espacio)
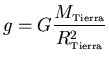 en esta última ecuación obtenemos que la velocidad de escape para
una órbita geoestacionaria (de radio igual a (8)) es
en esta última ecuación obtenemos que la velocidad de escape para
una órbita geoestacionaria (de radio igual a (8)) es
Puesto que la masa de la partícula que lanzamos es mucho menor que
la masa del satélite, podemos considerar que éste no varía su
velocidad de traslación (que sigue siendo (9)).
Medida con respecto al satélite, la velocidad de escape (11)
de la partícula será entonces
Para la útima parte del problema hay que tener en cuenta que la
fuerza gravitatoria, por ser central, no tiene momento con respecto al
centro de la órbita:
![]() (ya que
(ya que ![]() y
y
![]() son
antiparalelos).
Por ello, y teniendo en cuenta que el momento de una fuerza es lo que
hace cambiar con el tiempo al momento angular
son
antiparalelos).
Por ello, y teniendo en cuenta que el momento de una fuerza es lo que
hace cambiar con el tiempo al momento angular
![]() a través de
la ecuación
a través de
la ecuación
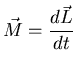 , entonces el momento
angular medido desde el centro de la órbita (desde La Tierra) para
el movimiento de la partícula es constante (que es la segunda ley
de Kepler)
, entonces el momento
angular medido desde el centro de la órbita (desde La Tierra) para
el movimiento de la partícula es constante (que es la segunda ley
de Kepler)
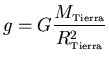 ,
obtenemos la siguiente ecuación de segundo grado
,
obtenemos la siguiente ecuación de segundo grado
![\begin{displaymath}
\left(\frac{v_{\scriptscriptstyle \rm cerca}}{v'}\right)^2
-...
...Tierra}^2}{v'^2 r_{\scriptscriptstyle \rm geo}}-1\right]=0\, .
\end{displaymath}](img40.png)
![${\displaystyle \frac{v_{\scriptscriptstyle \rm cerca}}{v'}=
\frac{\displaystyle...
...ptscriptstyle \rm Tierra}^2}{v'^2 r_{\scriptscriptstyle \rm geo}}-1\right]}{2}}$](img41.png) ,
nos interesa aquella que corresponde al punto más cercano a La
Tierra y por tanto a la velocidad mayor posible (signo + en el +/-),
ya que de acuerdo con (13), el producto del radio de la
órbita por la velocidad es una constante
,
nos interesa aquella que corresponde al punto más cercano a La
Tierra y por tanto a la velocidad mayor posible (signo + en el +/-),
ya que de acuerdo con (13), el producto del radio de la
órbita por la velocidad es una constante