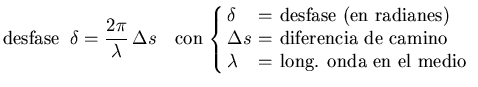
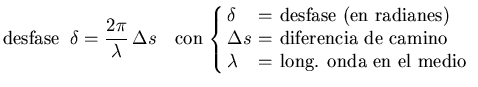
P.23
Sólo en los casos de reflexión (caso b) y caso e)) los pares de
fuentes son coherentes.
P.24
Para este problema, cuando se habla del rayo ``rojo'' y del rayo ``verde''
no se refiere a dos longitudes de onda distintas sino que, siempre con la
misma longitud de onda, el rayo ``rojo'' es el reflejado en la primera
superficie de separación y el rayo ``verde'' es el reflejado en la segunda.
Recordar que para una superficie que separa dos medios con índice
de refracción distintos, cuando la reflexión en tal superficie
tiene lugar dentro del medio donde la luz se propaga más
rápidamente (en el medio de menor índice de refracción)
entonces el rayo reflejado lleva un desfase de
![]() con respecto al rayo incidente.
O si queremos expresar este desfase como diferencia de camino, el rayo
reflejado lleva una diferencia de camino igual a
con respecto al rayo incidente.
O si queremos expresar este desfase como diferencia de camino, el rayo
reflejado lleva una diferencia de camino igual a ![]() con
respecto al rayo incidente.
Notar que la longitud de onda cambia dependiendo del índice de
refracción del medio: si denotamos por
con
respecto al rayo incidente.
Notar que la longitud de onda cambia dependiendo del índice de
refracción del medio: si denotamos por ![]() la longitud de
onda de la luz en el vacío, la longitud de onda
la longitud de
onda de la luz en el vacío, la longitud de onda ![]() dentro del
recubrimiento viene dada por
dentro del
recubrimiento viene dada por


P.25
A partir de la ecuación que relaciona el desfase (medido en
radianes) con la diferencia de camino,
 , un desfase de 180 grados
(
, un desfase de 180 grados
(![]() radianes) corresponde a una diferencia de camino
radianes) corresponde a una diferencia de camino
![]() .
Para una longitud de onda de 600nm esta diferencia de camino es
entonces 300nm.
Este misma diferencia de camino para una longitud de onda
.
Para una longitud de onda de 600nm esta diferencia de camino es
entonces 300nm.
Este misma diferencia de camino para una longitud de onda
![]() produce un desfase
produce un desfase
P.26
Puesto que tenemos que
![]() como en el
problema 24, entonces podemos
utilizar el resultado (32) para el desfase entre el rayo
reflejado en la superficie aceite-agua y el rayo reflejado en la
superficie aire-aceite
como en el
problema 24, entonces podemos
utilizar el resultado (32) para el desfase entre el rayo
reflejado en la superficie aceite-agua y el rayo reflejado en la
superficie aire-aceite
P.27
Repasemos primero el experimento de la doble rendija: cada rendija
difracta la luz monocromática incidente en todas las direcciones.
La diferencia de camino ![]() entre los dos rayos que interfieren
en la pantalla a una altura y viene dada aproximadamente por
entre los dos rayos que interfieren
en la pantalla a una altura y viene dada aproximadamente por
![]() si la distancia L entre la rendija y la pantalla
es mucho más grande que y.
si la distancia L entre la rendija y la pantalla
es mucho más grande que y.
 y por tanto
de (38) obtenemos que la posición
y por tanto
de (38) obtenemos que la posición
Para el problema, la separación entre dos máximos en la pantalla
es por tanto igual a
 o 1.2mm.
Luego en 10 milímetros (=1 centímetro) caben 10/1.2=8 máximos.
o 1.2mm.
Luego en 10 milímetros (=1 centímetro) caben 10/1.2=8 máximos.
P.28
Si hay 28 franjas brillantes (=máximos) en 1 centímetro la
separación entre dos máximos es 1cm/28.
Y aplicando (40) se obtiene que
P.29
Los fasores es una forma sencilla de representar gráficamente las
ecuaciones matemáticas que vamos a estudiar aquí en más
detalle.
Recordando la relación trigonométrica
![]() , la suma de los tres campos eléctricos, que tiene por
forma general
, la suma de los tres campos eléctricos, que tiene por
forma general
![]() se escribe
se escribe

P.30 y P.32
De acuerdo con el problema 27,
si la distancia L a la pantalla es lo suficientemente grande
comparada con la posición y sobre la pantalla, entonce ls
diferencia de camino para dos rayos consecutivos es
 , y por lo
tanto, el desfase correspondiente es
, y por lo
tanto, el desfase correspondiente es
 para tres
rendijas.
De la ecuación (44) está claro que la intensidad será
cero (=mínimo) para
para tres
rendijas.
De la ecuación (44) está claro que la intensidad será
cero (=mínimo) para

Las posiciones de máximo aparecen para
![]() , con intensidad
, con intensidad
![]() ,
,

P.31
Cuando se tapa una de las rendijas de los extremos, lo que queda son
dos rendijas separadas una distancia d.
Del resultado (38) del
problema 27, tenemos que el
máximo de orden m va a aparecer para un ángulo de
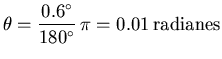 .
El que este ángulo esté medido desde la rendija del centro o desde
el punto medio entre dos rendijas no importa para un ángulo tan
pequeño.
El máximo de cuarto orden aparecerá por tanto para un ángulo de
.
El que este ángulo esté medido desde la rendija del centro o desde
el punto medio entre dos rendijas no importa para un ángulo tan
pequeño.
El máximo de cuarto orden aparecerá por tanto para un ángulo de
Cuando se cubre la rendija central, volvemos a quedarnos con dos
rendijas pero esta vez separadas una distancia 2d.
Luego el ángulo para el máximo de orden m vendrá dado por
la ecuación (47) pero con d sustituida por
d'=2d
![\begin{displaymath}
m\lambda=(2d) {\rm sen} \theta'
\rule[-3mm]{0.2mm}{5mm}_{\...
....2mm}{5mm}_{\scriptscriptstyle {\rm m\acute{a}ximo orden }m}
\end{displaymath}](img166.png)
P.43
Puesto que las dos fuentes son coherentes, el efecto del montaje del
problema es el de un experimento de
doble rendija, con las dos rendijas
separadas una distancia ![]() .
Si la pantalla está lo suficientemente alejada, la diferencia de
camino entre los dos rayos emitidos por cada foco es aproximadamente
.
Si la pantalla está lo suficientemente alejada, la diferencia de
camino entre los dos rayos emitidos por cada foco es aproximadamente
![]() , siendo este último resultado exacto si los dos rayos son
paralelos y se llevan a interferir sobre la pantalla a través de un
telescopio.
, siendo este último resultado exacto si los dos rayos son
paralelos y se llevan a interferir sobre la pantalla a través de un
telescopio.
En general, dos fuentes coherentes que tienen entre sí una
diferencia de fase igual a ![]() producen en el punto en el que
interfieren una intensidad
producen en el punto en el que
interfieren una intensidad