Problemas de polarización: 16-22

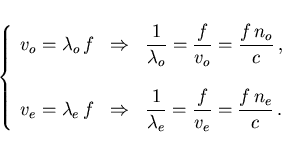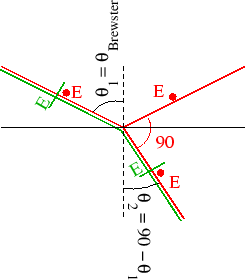
Antes de empezar los problemas, repasemos el concepto de ángulo de polarización, también llamado ángulo de Brewster.

Sea un rayo luminoso cuyo campo eléctrico tiene una componente que está oscilando en el plano de la página (E en color verde en la figura) y otra componente oscilando en perpendicular a la página (E en color rojo). Si el rayo al pasar de un medio a otro se refracta, y la relación entre el ángulo de incidencia $\theta_1$ y los índices de refracción de los dos medios es tal que el rayo refractado forma exactamente un ángulo de 90 grados con el rayo reflejado, entonces este rayo reflejado está completamente polarizado. Al ángulo de incidencia que cumple esto se llama ángulo de polarización o de Brestwer, y cumple

$$n_1 {\rm sen} \theta_1=n_2 {\rm sen} \hspace{-3mm} \unde... ....2mm}{5mm}_{\scriptscriptstyle \rm polar} =\frac{n_2}{n_1} .$$ (23)

P.16 y P.17 Sea $I_1$ la intensidad que deja pasar el primer polarizador: tras pasar el segundo polarizador, la intensidad será $I_2=I_1\cos^2\theta$ y tras pasar el tercer polarizador, la intensidad será

$$I_{\scriptscriptstyle \rm transmitida}=\left(I_1\cos^2\theta... ...\rm sen} ^2\theta} =\frac{I_1}{4} {\rm sen} ^2(2\theta) ,$$ (24)

utilizando que ${\rm sen} (2\theta)=2 {\rm sen} \theta\cos\theta$. La intensidad transmitida es máxima cuando ${\rm sen} (2\theta)$ es igual a uno, es decir, para $\theta=45^\circ$.

Para el problema 17, basta con sustituir $\theta$ por $\theta_0+\omega t$, donde $\theta_0$ es el ángulo que forma el eje de transmisión del segundo polarizador con respecto a la vertical; en nuestro caso, $\theta_0=0$

$$I_{\scriptscriptstyle \rm transmitida}=\frac{I_1}{4} {\rm sen} ^2(2\omega t) .$$ (25)

P.18 Tomando que el medio donde está el rayo incidente es el aire ($n_1\approx 1$), tenemos de acuerdo con lo explicado en el repaso que si para $\theta_1=60^\circ$ se produce la polarización del rayo reflejado, entonces el ángulo de refracción es $\theta_2=90^\circ-\theta_1=30^\circ$; y así el índice de refracción del segundo medio es

$$n_2=\tan\theta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm polar}=1.73 .$$ (26)

P.19 De la ecuación (11) ya sabemos que el ángulo crítico para un cambio de un medio 1 a un medio 2 viene dado por ${\displaystyle {\rm sen} \theta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm crit}=\frac{n_2}{n_1}}$. En nuestro caso, el segundo medio es el aire ($n_2\approx 1$) y como el ángulo crítico es 45 grados entonces el índice de refracción del primer medio es igual a

$${\rm sen} 45^\circ=\frac{1}{n_1}\quad\Rightarrow\quad n_1=\sqrt{2}=1.41 .$$

Si ahora tenemos un rayo incidiendo del medio 1 al aire, el ángulo de incidencia para el que el rayo reflejado (en el medio 1) está completamente polarizado viene dado por

$$\tan\theta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm ... ...]{0.2mm}{5mm}_{\scriptscriptstyle \rm polar}=35^\circ 16' ,$$ (27)

aplicando el resultado (23). Si por el contrario el rayo está incidiendo desde el aire sobre el medio 1, el ángulo de polarización cumple entonces que su tangente es la inversa de la del ángulo (27); y por tanto $\theta_2\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm polar}=54^\circ 44'$.

P.20 Para el paso del aire a cada uno de los medios, el ángulo de polarización viene dado por la ecuación (23)

$$\begin{array}{llcl} \mbox{agua}: & \theta_1\rule[-3mm]{0.2mm... ...ce{-2mm}& {\rm arctan} (1.5)=56^\circ 19' .\\ \end{array}$$ (28)

P.21 El rayo pasa de un medio de índice de refracción $n_1$ al aire ($n_2\approx 1$), luego el ángulo crítico viene dado por (11), ${\displaystyle {\rm sen} \theta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm crit}=\frac{1}{n_1}}$. Para el mismo cambio de medio, el ángulo de incidencia para que el rayo reflejado esté completamente polarizado es

$$\tan\theta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm ... ...eta_1\rule[-3mm]{0.2mm}{5mm}_{\scriptscriptstyle \rm crit} .$$ (29)

El anterior resultado lo podemos escribir como ${\displaystyle \frac{ {\rm sen} \theta_{\scriptscriptstyle \rm polar}}{\cos\t... ...riptscriptstyle \rm polar}} = {\rm sen} \theta_{\scriptscriptstyle \rm crit}}$, y puesto que el coseno siempre es menor o igual que uno, entonces

$${\rm sen} \theta_{\scriptscriptstyle \rm crit} =\frac{ {... ...r}}\geq {\rm sen} \theta_{\scriptscriptstyle \rm polar} .$$ (30)

Como la función seno es una función creciente, es decir, si crece el ángulo crece su seno, entonces del anterior resultado se deduce que el ángulo crítico es mayor que el ángulo de polarización.

P.22 Por la definición de índice de refracción, la velocidad de la luz en un medio de índice de refracción n es v=c/n, siendo c la velocidad de la luz en el vacío. Dentro de la lámina de calcita, el rayo con el campo eléctrico paralelo al eje óptico (oscilando en una dirección normal a la página) se propaga a una velocidad $v_e$ distinta a la velocidad $v_o$ del rayo cuyo campo eléctrico está oscilando en el plano de la página. Y por lo tanto, dentro de la calcita, la longitud de onda del primer rayo es distinta a la longitud de onda: puesto que la frecuencia f con la que oscila el campo eléctrico es siempre la misma (tanto dentro como fuera de la calcita), entonces tendremos que

$$\left\{\begin{array}{lcl} v_o=\lambda_o f &\Rightarrow& {\... ...bda_e}=\frac{f}{v_e} =\frac{f n_e}{c}} . \end{array}\right.$$

En el espesor t de la placa caben ${\displaystyle \frac{t}{\lambda_o}}$ longitudes de onda del rayo ordinario (el que oscila en el plano de la página) y ${\displaystyle \frac{t}{\lambda_e}}$ del rayo extraordinario (el que oscila paralelo al eje óptico, en este caso, perpendicular a la página). Las dos polarizaciones estaban en fase al entrar en la calcita; dentro de ella, la diferencia en el número de ondas que cabe en el espesor t para cada polarización nos dará el desfase entre estas dos polarizaciones cuando salgan de la calcita. Puesto que un diferencia de una longitud de onda corresponde a un desfase de $2\pi$ (=una oscilación completa), el desfase al salir de la placa es

$$\delta =2\pi\left(\frac{t}{\lambda_o}-\frac{t}{\lambda_e}\right)= \frac{2\pi f}{c} t (n_o-n_e) .$$ (31)