P.1
La ley de la reflexión nos dice que si ![]() es el ángulo que
forma el rayo incidente con la normal (=perpendicular) al espejo,
entonces el rayo reflejado forma también un ángulo
es el ángulo que
forma el rayo incidente con la normal (=perpendicular) al espejo,
entonces el rayo reflejado forma también un ángulo ![]() con la
normal.
Por tanto, el ángulo que forma el rayo reflejado con el incidente es
de
con la
normal.
Por tanto, el ángulo que forma el rayo reflejado con el incidente es
de ![]() .
.
Si ahora, sin mover el rayo el incidente, giramos el espejo un
ángulo ![]() (y por tanto, normal al espejo también gira el
mismo ángulo), entonces el ángulo de incidencia será de
(y por tanto, normal al espejo también gira el
mismo ángulo), entonces el ángulo de incidencia será de
![]() , y el ángulo de reflexión también será
, y el ángulo de reflexión también será
![]() .
El rayo reflejado con respecto al incidente forma un ángulo de
.
El rayo reflejado con respecto al incidente forma un ángulo de
![]() , o lo que es lo mismo, ha aumentado en
, o lo que es lo mismo, ha aumentado en ![]() con
respecto al primer caso.
con
respecto al primer caso.
P.2
Es un resultado teórico que para incidencia normal (=en perpendicular)
sobre una superficie que separa un medio 1 de un medio 2, la
intensidad del rayo reflejado está relacionada con la intensidad del
rayo incidente a través de
Para nuestro caso, la fracción de energía (=de intensidad) viene
dada por
P.3
Del resultado teórico (1), la intensidad reflejada y la
intensidad transmitida (=refractada) en un cambio de medio con
incidencia normal vienen dadas, respectivamente, por el producto de la
intensidad incidente ![]() por el factor R de reflexión o por
el factor T de transmisión
por el factor R de reflexión o por
el factor T de transmisión
Para calcular la intensidad transmitida por una placa de vidrio, hay que considerar todas las reflexiones, y sus correspondientes factores de reflexión, que se van a producir en el interior del vidrio. En la figura se han representado las primeras de estas reflexiones; los colores y el que los rayos no sean completamente perpendiculares a las superficies del vidrio son sólo para facilitar la comprensión de la figura.
Hay que notar que si además la luz tiene la suficientemente coherencia, la interferencia entre los rayos transmitidos dentro del vidrio y los rayos reflejados dentro de este medio también influye en la intensidad de la luz que sale al aire. Aproximadamente entonces, la intensidad transmitida al aire es (n es
el índice de refracción del vidrio) es normalmente bastante
pequeño: por ejemplo para n=1.5 es igual a R=0.11.
(n es
el índice de refracción del vidrio) es normalmente bastante
pequeño: por ejemplo para n=1.5 es igual a R=0.11.
Del resultado (4) se ve que el factor de transmisión de la
lámina de vidrio es aproximadamente ![]() , o si despreciamos
la pequeña correción
, o si despreciamos
la pequeña correción ![]() , igual a
, igual a ![]() con
con
 .
.
P.4
Por la definición de índice de refracción de un medio
P.5
La frecuencia de una onda de luz monocromática no varía al
cambiar de medio: es la frecuencia con la que oscila el campo
electromagnético que es la luz y es la misma frecuencia con la que
la luz hace oscilar las partículas cargadas del medio que
atraviesa y es también la misma frecuencia con la que estas
partículas excitadas radian ondas electromagnéticas.
Puesto que la longitud de onda y la frecuencia están relacionadas
con la velocidad de la luz a través de

Los colores que vemos son producto de una reacción química en
las células oculares llamadas conos: estas células reaccionan a la
energía de los fotones de luz que les llegan.
Puesto que la energía de un fotón de luz sólo depende de su
frecuencia, y ya que la frecuencia no depende del medio por el que se
propague la luz, entonces el buceador dentro del agua sigue viendo el
mismo color rojo que si estuviera fuera del agua.
P.7 La ley de la refracción (Ley de Snell) establece que si:
 , entonces puede
ocurrir que para un ángulo de incidencia
, entonces puede
ocurrir que para un ángulo de incidencia
P.8
Muy similar al
problema anterior pero
ahora con
![]() y
y
![]() : el ángulo crítico
es entonces
: el ángulo crítico
es entonces
P.9
Sea h=5m la profundidad a la que está el foco luminoso y sea
r la distancia sobre la superficie del agua medida desde la
vertical que pasa por el foco luminoso: el seno del ángulo de
incidencia de un rayo que saliendo de ese foco llega a un punto de la
circunferencia de radio r es
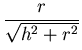 ,
como se puede demostrar con un dibujo simple.
Si este seno es menor que
,
como se puede demostrar con un dibujo simple.
Si este seno es menor que
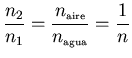 entonces
todavía se produce refracción y por tanto saldrá luz al aire
proveniente del foco submergido.
El radio R para el que justo se cumple la condición límite
marca es
entonces
todavía se produce refracción y por tanto saldrá luz al aire
proveniente del foco submergido.
El radio R para el que justo se cumple la condición límite
marca es
P.10
Muy similar al
problema anterior: la
trayectoria que siguen los rayos luminosos que llegan desde el
exterior hasta el nadador submergido es la misma que la de los rayos
que salieran del nadador para llegar fuera del agua.
Luego el resultado es (13), con h=3m y n=1.33.
P.11
Por la figura está claro que el ángulo que forma el rayo incidente
con el lado inclinado del prisma es 45 grados y por tanto, el ángulo
que forma con la normal (ángulo de incidencia) es también 45
grados.
De acuerdo con el resultado (10), reflexión total se
producirá si
P.12
Sea h=3cm es espesor de la placa de vidrio de índice de
refracción n=1.5 y ![]() =40 grados el ángulo de incidencia.
De la figura siguiente obtenemos que para la refracción en el paso
del aire al vidrio se cumple que
=40 grados el ángulo de incidencia.
De la figura siguiente obtenemos que para la refracción en el paso
del aire al vidrio se cumple que

 .
Por lo tanto combinando estos dos resultados
.
Por lo tanto combinando estos dos resultados
P.13 De la figura se ve que la distancia d que se pide es igual a

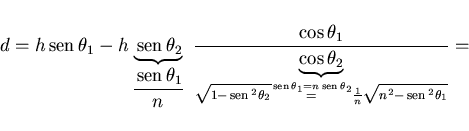
P.14
Puesto que el índice de refracción del aire (=vacío) es
igual a uno para todas las longitudes de onda, tenemos
P.15
De la figura, y debido a la simetría del problema, el ángulo de
desviación entre el rayo incidente y el rayo refractado,
![]() ,
es igual a la mitad de la desviación total que se pide en el
problema:
,
es igual a la mitad de la desviación total que se pide en el
problema:
![]() .
.
Para el caso particular que se pide,
![]() y
y
![]() luego
luego