
Importante. No confundir la rendija única de anchura a, que es lo que acabamos de ver, con la
doble rendija formada por dos
rendijas separadas una distancia d o con la generalización de
la doble rendija, la
red de difracción:
mientras que
![]() (con m entero distinto de
cero) indica los ángulos para intensidad cero en la
difracción de Fraunhofer, la relación
(con m entero distinto de
cero) indica los ángulos para intensidad cero en la
difracción de Fraunhofer, la relación
![]() (con
m entero cualquiera) da los ángulos para máximo en una
doble rendija o en una red de difracción.
(con
m entero cualquiera) da los ángulos para máximo en una
doble rendija o en una red de difracción.
En la ecuación (54) acabamos de ver la condición para
intensidad cero en la luz difractada por una rendija (infinitamente
larga) de anchura a.
Para un ángulo ![]() tal condición no se cumple, ya que no
hay ningún desfase entre los rayos que salen de cada punto de la
rendija.
Luego para
tal condición no se cumple, ya que no
hay ningún desfase entre los rayos que salen de cada punto de la
rendija.
Luego para ![]() habrá un máximo de intensidad, llamado
máximo principal.
La distancia sobre una pantalla (suficientemente alejada) entre el
máximo principal y el primer mínimo ocurre para un ángulo
habrá un máximo de intensidad, llamado
máximo principal.
La distancia sobre una pantalla (suficientemente alejada) entre el
máximo principal y el primer mínimo ocurre para un ángulo
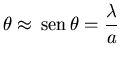 .
De acuerdo con el criterio de Rayleigh, este ángulo también
corresponde al ángulo más pequeño que dos rendijas pueden estar
separadas de forma que sobre la pantalla podamos resolver las dos rendijas.
Esto se llama la separación angular crítica o el ángulo
límite de resolución
.
De acuerdo con el criterio de Rayleigh, este ángulo también
corresponde al ángulo más pequeño que dos rendijas pueden estar
separadas de forma que sobre la pantalla podamos resolver las dos rendijas.
Esto se llama la separación angular crítica o el ángulo
límite de resolución
P.33
Para una única rendija de anchura a, las posiciones de mínimo
en la pantalla aparecen para ángulos ![]() que cumplen
que cumplen
![]() .
Por otra parte, el ángulo
.
Por otra parte, el ángulo ![]() que apunta hacia el punto sobre la
pantalla donde aparece el mínimo de orden m, punto que
está a una distancia
que apunta hacia el punto sobre la
pantalla donde aparece el mínimo de orden m, punto que
está a una distancia ![]() medida desde el centro de la pantalla (el
centro de la pantalla se toma como el punto de corte con la pantalla
de la normal trazada a la rendija), viene dado por
medida desde el centro de la pantalla (el
centro de la pantalla se toma como el punto de corte con la pantalla
de la normal trazada a la rendija), viene dado por
 , con L la distancia entre la
rendija y la pantalla.
Para una distancia sobre la pantalla mucho más pequeña que
L, se puede escribir
, con L la distancia entre la
rendija y la pantalla.
Para una distancia sobre la pantalla mucho más pequeña que
L, se puede escribir
 .
El primer cero de intensidad en la derecha aparece para una posición
sobre la pantalla de
.
El primer cero de intensidad en la derecha aparece para una posición
sobre la pantalla de
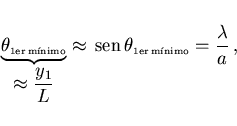
P.34
La primera cuestión está contestada en el
problema anterior: la
anchura del máximo central es la distancia entre el primer
mínimo a la derecha y el primer mínimo a la izquierda,
distancia dada por (57).
Si ahora la anchura de la rendija que abrimos sobre la pantalla es
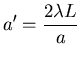 , entonces la anchura del máximo
sobre un plano colocado sobre la primera rendija es
, entonces la anchura del máximo
sobre un plano colocado sobre la primera rendija es
P.35
Para una abertura circular de diámetro D=0.1mm iluminada por
una luz de longitud de onda ![]() =700nm, el ángulo bajo el que
se ve el primer mínimo viene dado por (54) con la
corrección de incluir el factor 1.22 correspondiente a una abertura
circular
=700nm, el ángulo bajo el que
se ve el primer mínimo viene dado por (54) con la
corrección de incluir el factor 1.22 correspondiente a una abertura
circular
P.36
La separación entre los faros es y=112cm y el ángulo bajo
el que vemos los dos focos a una distancia L es approximadamente
![]() =y/L.
Por lo tanto el ángulo mínimo que pueden estar separados, o lo
que es lo mismo, la mayor distancia L posible a la que los
podemos observar a través del ojo (una abertura circular de
diámetro D=5mm), viene dada por (56)
=y/L.
Por lo tanto el ángulo mínimo que pueden estar separados, o lo
que es lo mismo, la mayor distancia L posible a la que los
podemos observar a través del ojo (una abertura circular de
diámetro D=5mm), viene dada por (56)
P.37 y P.38
Repaso del funcionamiento de la red de difracción
aquí.
Todas las longitudes de onda de una luz incidente perpendicularmente
sobre una red de difracción es difractada en todas las direcciones.
Para una longitud de onda determinada ![]() , en aquellas
direcciones en la que se cumpla
, en aquellas
direcciones en la que se cumpla
Para el problema 37, la separación entre dos rendijas en la red es
d=1cm/2000.
Aplicando (61) se obtiene que en el primer orden (m=1)
la línea para ![]() =410nm se verá para un ángulo de
4 grados y 42 minutos, y de 4 grados y 59 minutos para la otra línea.
=410nm se verá para un ángulo de
4 grados y 42 minutos, y de 4 grados y 59 minutos para la otra línea.
En el problema 38 la longitud de onda en primer orden es 486nm para
un ángulo de 0.0972 radianes, y de 660nm para el otro ángulo.
P.39
Volviendo a utilizar la ecuación de interferencia constructiva,
![]() , para la red de difracción, obtenemos que
en primer orden (m=1) para una red con d=1cm/2000
, para la red de difracción, obtenemos que
en primer orden (m=1) para una red con d=1cm/2000
P.40
En una red de difracción, el máximo ángulo de difracción es 90
grados, es decir, cuando el rayo difractado sale tangente a la red.
En orden m, tal ángulo corresponde a una longitud de onda
P.41
Puesto que la resolución es igual al número de orden multiplicado
por el número de rendijas de la red iluminadas (se considera que se
está iluminando toda la red), en nuestro caso en que la resolución
es 22000 en el cuarto orden, el número de rendijas es 22000/4=5500,
que hay por cada 5cm de lado.
Luego la distancia entre rendijas es d=5cm/5500 y el ángulo
en cuarto orden para la longitud de onda dada es
P.42
Como se ve en la figura, la diferencia de camino entre dos rayos
difractados en dos rendijas consecutivas es
![]() .
.