P.33
Tenemos un campo magnético ![]() de módulo constante
B=3.6T y apuntando hacia dentro de la página.
Si por el conductor de la figura, que tiene una densidad de masa
de módulo constante
B=3.6T y apuntando hacia dentro de la página.
Si por el conductor de la figura, que tiene una densidad de masa
![]() , circula una corriente
, circula una corriente ![]() en sentido de
izquierda a derecha, la fuerza que está ejerciendo el campo
magnético sobre un elemento diferencial de longitud
en sentido de
izquierda a derecha, la fuerza que está ejerciendo el campo
magnético sobre un elemento diferencial de longitud ![]() del
conductor es igual a
del
conductor es igual a
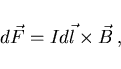
P.34
El campo magnético creado por un conductor rectilíneo infinito a
una distancia r en perpendicular al conductor es igual a
 ; esto se calcula por la Ley de
Ampère como en los problemas
30 y
31, o bien por aplicación
directa de la Ley de Biot-Savart como en el
problema 28.
La fuerza que está haciendo el conductor infinito a un elemento
; esto se calcula por la Ley de
Ampère como en los problemas
30 y
31, o bien por aplicación
directa de la Ley de Biot-Savart como en el
problema 28.
La fuerza que está haciendo el conductor infinito a un elemento
![]() de otro conductor paralelo a una distancia
r=2mm es igual a
de otro conductor paralelo a una distancia
r=2mm es igual a
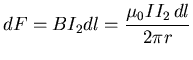 , donde
, donde ![]() es la corriente que
circula por este segundo conductor; la dirección de
es la corriente que
circula por este segundo conductor; la dirección de ![]() es radial.
Si este último conductor tiene una longitud L=30cm entonces
la fuerza total ejerciada sobre él es
es radial.
Si este último conductor tiene una longitud L=30cm entonces
la fuerza total ejerciada sobre él es

35
La fuerza ejercida sobre el segmento paralelo al eje X, que tiene
una longitud de
![]() es igual a
es igual a

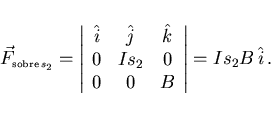
P.36
Puesto que tanto ![]() como el vector
como el vector ![]() son constantes, entonces
son constantes, entonces
P.37
El campo magnético creado por el conductor infinito a una distancia
r en perpendicular de él ya ha sido calculado varias veces y es
igual a
 , con
, con
![]() ; su
sentido es hacia afuera a la parte izquierda del conductor, y hacia
adentro a la derecha de él.
Para cada uno los 2 tramos paralelos al conductor infinito, la fuerza se
calcula inmediatamente ya que el campo magnético creado por el
conductor infinito es igual en todos los puntos de cada tramo: así
; su
sentido es hacia afuera a la parte izquierda del conductor, y hacia
adentro a la derecha de él.
Para cada uno los 2 tramos paralelos al conductor infinito, la fuerza se
calcula inmediatamente ya que el campo magnético creado por el
conductor infinito es igual en todos los puntos de cada tramo: así
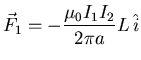 ,
donde L=10cm es la longitud del tramo e
,
donde L=10cm es la longitud del tramo e  .
.
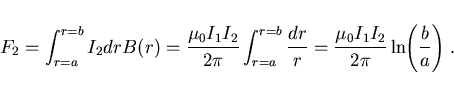
P.38 y P.40
Una partícula de carga q moviéndose con una velocidad
![]() (por ejemplo hacia la derecha en esta hoja) dentro de un campo
magnético uniforme perpendicular a la velocidad (por ejemplo hacia
adentro de esta hoja) esta sometida a una fuerza igual a
(por ejemplo hacia la derecha en esta hoja) dentro de un campo
magnético uniforme perpendicular a la velocidad (por ejemplo hacia
adentro de esta hoja) esta sometida a una fuerza igual a
![]() , que lleva dirección perpendicular
tanto a
, que lleva dirección perpendicular
tanto a ![]() como a
como a ![]() (en nuestro caso, hacia arriba de
la página).
Esta fuerza no hace trabajo ya que es perpendicular a la velocidad y
por tanto a un desplazamiento
(en nuestro caso, hacia arriba de
la página).
Esta fuerza no hace trabajo ya que es perpendicular a la velocidad y
por tanto a un desplazamiento
![]() : así la
fuerza no varía la energía cinética de la partícula, no
varía el módulo de su velocidad.
Esta fuerza es una fuerza centrípeta y por tanto el radio R de
la trayectoria circular que va a llevar la partícula está
relacionado con su velocidad de acuerdo con
: así la
fuerza no varía la energía cinética de la partícula, no
varía el módulo de su velocidad.
Esta fuerza es una fuerza centrípeta y por tanto el radio R de
la trayectoria circular que va a llevar la partícula está
relacionado con su velocidad de acuerdo con
P.39
La velocidad tiene una componente ![]() paralela a la
dirección de
paralela a la
dirección de ![]() , componente sobre la que no actúa la Fuerza
de Lorentz (el producto vectorial de esta componente de la velocidad
por el vector
, componente sobre la que no actúa la Fuerza
de Lorentz (el producto vectorial de esta componente de la velocidad
por el vector ![]() es cero al ser los dos vectores paralelos) y
por tanto, componente que no cambia en módulo.
La componente de la velocidad perpendicular al campo magnético, esto
es
es cero al ser los dos vectores paralelos) y
por tanto, componente que no cambia en módulo.
La componente de la velocidad perpendicular al campo magnético, esto
es
![]() , es la que produce un movimiento circular tal
y como hemos visto en el
problema anterior.
La trayectoria que sigue la partícula por lo tanto es una espiral:
la partícula va trazando una circunferencia y a la vez se va
desplazando a lo largo de la dirección de
, es la que produce un movimiento circular tal
y como hemos visto en el
problema anterior.
La trayectoria que sigue la partícula por lo tanto es una espiral:
la partícula va trazando una circunferencia y a la vez se va
desplazando a lo largo de la dirección de ![]() con una velocidad
con una velocidad
![]() .
Al cabo de una vuelta, las componentes de la velocidad vuelven a estar
en la misma dirección que al inicio, y por la ecuación
(62), el tiempo que se requiere para dar esa vuelta es
.
Al cabo de una vuelta, las componentes de la velocidad vuelven a estar
en la misma dirección que al inicio, y por la ecuación
(62), el tiempo que se requiere para dar esa vuelta es
 , tiempo durante el que la partícula
cargada se ha desplazado una distancia
, tiempo durante el que la partícula
cargada se ha desplazado una distancia