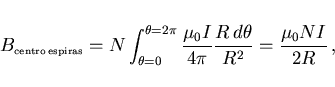P.30
La simetría del campo magnético en este problema es
la siguiente: puesto que para puntos alejados de los extremos podemos
considerar al cable como infinito, entonces ![]() se ``enrolla''
en circunferencias alrededor del cable coaxial, dependiendo su
intensidad en un punto P sólo de la distancia que separa a dicho punto
del eje del cable.
Esto nos permite utilizar la Ley de Ampère, integrando
se ``enrolla''
en circunferencias alrededor del cable coaxial, dependiendo su
intensidad en un punto P sólo de la distancia que separa a dicho punto
del eje del cable.
Esto nos permite utilizar la Ley de Ampère, integrando
 a lo largo de una circunferencia
C de radio r que esté puesta perpendicularmente al cable y con
centro en el cable.
De esta forma, y por lo dicho para la simetría de
a lo largo de una circunferencia
C de radio r que esté puesta perpendicularmente al cable y con
centro en el cable.
De esta forma, y por lo dicho para la simetría de ![]() para
este problema, podemos escribir
para
este problema, podemos escribir

P.31
La simetría del campo magnético ![]() es la misma
que en el problema anterior y por tanto podemos seguir utilizando el
resultado anterior
es la misma
que en el problema anterior y por tanto podemos seguir utilizando el
resultado anterior
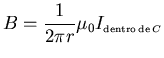 .
Para
.
Para ![]() ningún punto en el interior de C es atravesado por
corriente y por tanto
ningún punto en el interior de C es atravesado por
corriente y por tanto
![]() .
Para
.
Para ![]() la fracción de corriente que atraviesa el interior de
C es igual a
la fracción de corriente que atraviesa el interior de
C es igual a
 y por tanto
y por tanto
 .
Y para
.
Y para ![]() , es decir, en el exterior de la corteza, es toda la
intensidad
, es decir, en el exterior de la corteza, es toda la
intensidad ![]() la que atraviesa C.
Así
la que atraviesa C.
Así
P.32
Es la práctica de laboratorio de medir el campo magnético
terrestre.
El campo creado por N espiras de radio R en su centro es
igual a