

Una integral útil:
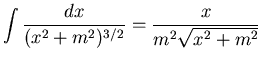 ,
con
,
con ![]() una constante.
una constante.
P.25
El conductor en forma de cigüeñal tiene una longitud
a=1cm en el tramo corto vertical y una longitud 2b=2cm
en el tramo corto horizontal. Por el condcutor circula una corriente
I=8A.
El tramo más largo que está alineado con el punto P donde
queremos calcular el campo magnético no produce ninguna
contribución al campo en P debido al producto vectorial en la
definición de
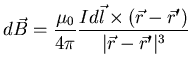 :
el elemento diferencial de longitud
:
el elemento diferencial de longitud ![]() de este tramo más largo es
paralelo al vector de posición
de este tramo más largo es
paralelo al vector de posición
![]() que va desde
que va desde ![]() hasta el punto P.
hasta el punto P.
El campo ![]() en P va hacia dentro de la página y es la suma
de las contribuciones de cada uno de los tramos cortos.
El tramo vertical produce un campo en P igual a
en P va hacia dentro de la página y es la suma
de las contribuciones de cada uno de los tramos cortos.
El tramo vertical produce un campo en P igual a
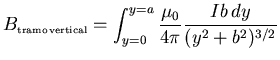 .
Y el horizontal
.
Y el horizontal
 .
La suma de las contribuciones de los tramos cortos es por tanto
.
La suma de las contribuciones de los tramos cortos es por tanto
P.26
El tramo circular tiene un radio R=20cm y por todo
el conductor circula una corriente I=15A.
Este problema es más sencillo que el anterior ya que cada elemento
diferencial de longitud en el tramo circular es perpendicular al
vector de posición ![]() que va desde ese elemento a P.
Como en el problema anterior, el tramo largo alineado con P no
produce ningún campo en P.
Éste es igual a
que va desde ese elemento a P.
Como en el problema anterior, el tramo largo alineado con P no
produce ningún campo en P.
Éste es igual a
P.27
Supongamos que la corriente circula por el arco exterior en
sentido antihorario. El campo creado por el arco exterior en P va
hacia fuera mientras que el creado por el arco interior. Puesto que
los dos tramos cortos horizontales alineados con P no producen nada
de campo magnético en P, y ya que los radios de cada uno de los
arcos es conocido, aplicando el resultado (49) del
problema anterior obtenemos
P.28
La espira circular tiene un radio R=10cm y el
campo creado por ella en su centro P tiene un módulo


P.29
Sólo el tramo horizontal de longitud 2a crea campo
magnético en el punto P, mientras que los dos tramos inclinados
no lo hacen ya que P está sobre cada una de las líneas
prolongación de los tramos inclinados.
La contribución del tramo horizontal viene dada por


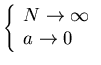 manteniendo el perímetro
N2a finito, o sea, convertimos el polígono en una
circunferencia, entonces en el resultado anterior obtendremos
manteniendo el perímetro
N2a finito, o sea, convertimos el polígono en una
circunferencia, entonces en el resultado anterior obtendremos