

Antes de empezar con los problemas de esta sección, consideremos una carga
puntual q situada en el origen de coordenadas y calculemos el
potencial creado por tal carga en un punto P situado a
una distancia R de la carga.
El campo eléctrico creado por esta carga a una distancia r
cualquiera es
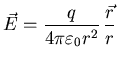 .
La diferencia de potencial entre un punto alejado infinitamente (al que se le asigna un potencial igual a cero) y el punto que estamos considerando es la
siguiente integral a través de un camino en dirección radial desde
el punto P hasta el infinito
.
La diferencia de potencial entre un punto alejado infinitamente (al que se le asigna un potencial igual a cero) y el punto que estamos considerando es la
siguiente integral a través de un camino en dirección radial desde
el punto P hasta el infinito
 .
.
P.17
Empecemos con la carga ![]() , que a una distancia r crea un
potencial (=energía potencial por unidad de carga) igual a
, que a una distancia r crea un
potencial (=energía potencial por unidad de carga) igual a
 : el traer una carga
: el traer una carga
![]() desde el infinito hasta una distancia
desde el infinito hasta una distancia ![]() de la carga
de la carga ![]() hace que el sistema adquiera una energía potencial de
hace que el sistema adquiera una energía potencial de
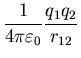 .
Si traemos ahora otra carga
.
Si traemos ahora otra carga ![]() desde el infinito hasta un punto que
está a una distancia
desde el infinito hasta un punto que
está a una distancia ![]() de la carga
de la carga ![]() y a una distancia
y a una distancia
![]() de la carga
de la carga ![]() , el aumento en energía potencial será
, el aumento en energía potencial será
 .
Por tanto lo que ha ganado en energía potencial el sistema durante
este proceso es
.
Por tanto lo que ha ganado en energía potencial el sistema durante
este proceso es
P.18
Dividamos el disco en anillos concéntricos de radio r y grosor
dr: si el punto P donde queremos calcular el potencial
está a una distancia x sobre el eje del disco,
cada elemento de tal anillo de radio r está a una distancia
![]() del punto P y por tanto el potencial creado
por el anillo en P es
del punto P y por tanto el potencial creado
por el anillo en P es
P.19
Puesto que el potencial a una distancia a=2.5m se toma como
cero, lo que nos están pidiendo en el problema es la diferencia de
potencial entre un punto cualquiera y un punto situado a a de la
línea cargada.
Consideraremos que el punto P donde queremos calcular tal diferencia
de potencial está situado sobre el plano XY a una distancia
r en perpendicular a la línea infinita de carga.
Consideremos un elemento diferencial de longitud dz de esta línea,
elemento situado a una distancia ![]() del origen de coordenadas y por
lo tanto alejado una distancia
del origen de coordenadas y por
lo tanto alejado una distancia
![]() del punto P:
la diferencia de potencial creada por tal elemento dz es
del punto P:
la diferencia de potencial creada por tal elemento dz es
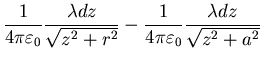 ya que la carga que lleva dz es
ya que la carga que lleva dz es ![]() con
con
![]() la densidad lineal de carga, que
es constante.
La diferencia de potencial que piden en el problema es por tanto
la densidad lineal de carga, que
es constante.
La diferencia de potencial que piden en el problema es por tanto

P.20
Sea un elemento diferencial dx' situado a una distancia x'
del origen, portador de una carga ![]() con
con ![]() la densidad
lineal de carga.
Tal elemento crea un potencial
la densidad
lineal de carga.
Tal elemento crea un potencial
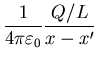 en un punto situado a una distancia x del origen,
fuera de la barra, y por tanto separado una distancia x-x' del elemento
diferencial dx'.
Así el potencial en x debido a toda la barra será la
suma(=integral) de las contribuciones de cada elemento diferencial
en un punto situado a una distancia x del origen,
fuera de la barra, y por tanto separado una distancia x-x' del elemento
diferencial dx'.
Así el potencial en x debido a toda la barra será la
suma(=integral) de las contribuciones de cada elemento diferencial
P.21
En (34) ya se ha calculado el potencial creado por un anillo de
carga uniforme q (con
![]() ) y radio r (con
r=0.1m) a una distancia x sobre el eje
) y radio r (con
r=0.1m) a una distancia x sobre el eje
P.22
Puesto que el campo electrostático es conservativo y ya que las
cargas no tienen velocidad inicial, la energía potencial que tiene
cada una de las cargas inicialmente sobre el cuadrado es igual a la
energía cinética final con la que llegan al infinito (en el
infinito la energía potencial es cero).
Para la primera carga que sale tenemos que inicialmente está bajo la
acción del potencial de las otras tres cargas (ver
problema 17), luego
P.23
Este problema se resuelve siguiendo los mismos pasos que en el
problema 15.
Por la simetría radial del problema, ![]() lleva dirección
radial y la Ley de Gauss la aplicaremos a una esfera de radio r,
concéctrica con la bola cargada
lleva dirección
radial y la Ley de Gauss la aplicaremos a una esfera de radio r,
concéctrica con la bola cargada

 y es constante, entonces
y es constante, entonces
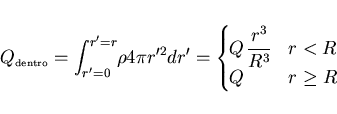
P.24
Este problema es similar al
problema 15,
con la sustitución
![]() .
.