Problemas de aplicación de la Ley de Gauss: 10-11, 13-16

${\displaystyle \oint_S\vec{E}\cdot d\vec{S} =\frac{Q_{\scriptscriptstyle {\rm ... ...ilon_0}\quad \mbox{con}\; d\vec{S}\mbox{: vector elem. diferencial de superf.}}$

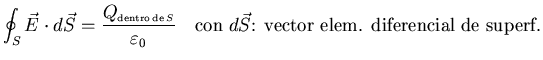
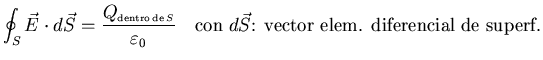
P.10 En los problemas en los que se quiera utilizar la Ley de Gauss, lo primero es estudiar qué simetría tiene el campo eléctrico $\vec{E}$: esférica (si radialmente sale de, o apunta hacia, un único punto), cilíndrica, ... A continuación se aplica la Ley de Gauss eligiendo con ``ojo'' como superficie de integración S una superficie cerrada que tenga una simetría lo más parecida a la del campo eléctrico: así $\vec{E}$ tendrá la misma dirección que el vector $d\vec{S}$, ${\vec{E}\cdot d\vec{S}=E dS}$, y además $\vec{E}$ tendrá el mismo valor en todos los puntos de dicha superficie con lo que ${\displaystyle \oint_S\vec{E}\cdot d\vec{S}=E\oint_S dS}$. Notar que no siempre se va a poder escoger una superficie cerrada que cumpla esta propiedad para todos sus puntos. Sin embargo, si el campo eléctrico tiene la suficiente simetría, sí que se va a poder elegir una superficie cerrada tal que la propiedad de arriba se cumpla para muchos de sus puntos, mientras que para el resto de los puntos de la superficie sobre la que integramos se obtenga que ${\vec{E}\perp d\vec{S}}$ y estos últimos puntos no den ninguna contribución a $\oint_S\vec{E}\cdot d\vec{S}$. Ver por ejemplo el problema 11 y el problema 13.

En nuestro caso, puesto que la distribución de carga es uniforme, la dirección del campo eléctrico es radial y por lo tanto la superficie más útil para aplicar sobre ella el teorema de Gauss es una esfera

$$\oint_{S={\scriptscriptstyle \rm esfera}}\vec{E}\cdot d\vec{S} =E_r 4\pi r^2 ,$$

con r el radio de la esfera. Lo único que queda por resolver es la carga que queda dentro de la superficie cerrada sobre la que hemos integrado:

• Si la esfera sobre la que estamos integrando tiene un radio menor que $R_1$, no contiene nada da carga.
• Si la esfera de radio r contiene la corteza interior pero no llega a la corteza exterior, $R_1<r<R_2$, entonces dentro de la superficie cerrada de integración hay una carga $q_1$.
• Si la superficie $S$ cerrada ontiene a las dos cortezas, $r>R_2$, entonces la carga en su interior es $q_1+q_2$.

$$E_r=\hspace{-1mm}\left\{ \begin{array}{ll} 0 & r<R_1 ,\\ ... ...ac{q_1+q_2}{\varepsilon_0}} & r\geq R_2 . \end{array}\right.$$ (18)

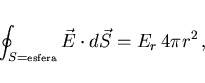
P.11 De forma similar al problema anterior, la distribución uniforme de carga hace que $\vec{E}$ lleve dirección radial y perpendicular al eje del cilindro: a) $\vec{E}$ vale lo mismo en módulo para todos los puntos que estén a la misma distancia del eje del cilnindro, y b) por tratarse de un cilindro de longitud infinita, $\vec{E}$ no tiene componente paralela al eje del cilindro. Una manera de ver esta última propiedad es darse cuenta que puesto que el cilindro es infinito y su carga está distribuida uniformemente, tenemos tanta carga a lo largo del eje a la izquierda de un punto cualquiera como a su derecha; y por lo tanto, la componente longitudinal a lo largo del eje creada por la parte izquierda se compensa con la creada por la parte derecha. Otra manera es a través de un argumento que se discutirá en el siguiente problema.

La superficie cerrada de integración es en este caso un cilindro de radio r, concéntrico con el cilindro cargado, longitud L y cerrado por dos tapas perpendiculares al eje del cilindro. Ya que la dirección de $\vec{E}$, al ser radial, es perpendicular al vector $d\vec{S}$ de las dos tapas, entonces

$$\oint_{S={\scriptscriptstyle \rm cilindro con tapas}} \vec... ...r\int_{S={\scriptscriptstyle \rm lateral}}dS}= E_r 2\pi rL .$$

Como en el problema anterior, para terminar de aplicar la Ley de Gauss sólo queda por calcular la carga que queda dentro de este cilindro cerrado con tapas: para $r<R_1$ no hay carga dentro ya que la superficie cargada más cercana está fuera; para $R_1<r<R_2$, una parte de longitud lateral L de la superficie cargada interior queda dentro del cilindro con tapas sobre el que estamos integrando, luego ${\displaystyle Q_{\scriptscriptstyle {\rm dentro de} S}=2\pi R_1 L\sigma_1}$; y por último, para $r>R_2$ la superficie de integración contiene una parte de longitud lateral L tanto de la superficie cargada interior como de la exterior, luego ${\displaystyle Q_{\scriptscriptstyle {\rm dentro de} S}=2\pi R_1 L\sigma_1+2\pi R_2 L\sigma_2}$. Recordar que la superficie lateral de un cilindro de radio R y longitud L es $2\pi RL$. Con todo esto tenemos

$$E_r=\hspace{-1mm}\left\{ \begin{array}{rcll} && 0& r<R_1 ,... ...+R_2\sigma_2}{\varepsilon_0 r}} & r>R_2 . \end{array}\right.$$ (19)

Y la relación entre las densidades de carga de las dos superficies para que el campo en el exterior $r>R_2$ sea cero debe ser

$$\sigma_2=-\frac{R_1}{R_2}\sigma_1 ,$$ (20)

y como es lógico, de signo opuesto.

P.13 El campo eléctrico creado por un plano infinito cargado con una densidad superficial de carga $\sigma$ uniforme se puede calcular aplicando la Ley de Gauss. Por simetría, la dirección esta vez de $\vec{E}$ tiene que ser perpendicular al plano y con sentido hacia afuera del plano si éste está cargado positivamente o con sentido apuntando al plano si la carga es negativa.

Esto se deduce del siguiente argumento: el plano por ser infinito tiene la simetría de que si giramos cualquier ángulo $\beta$ en torno a un eje que corte perpendicularmente al plano en cualquiera de sus puntos, el plano permanece invariante; por supuesto, esto funciona siempre que la distribución de carga en el plano sea uniforme. Ahora supongamos que la dirección del campo $\vec{E}$ no es exactamente perpendicular al plano, es decir, forma un ángulo ${\alpha\neq 0}$ con un eje que corte perpendicularmente al plano (ver figura). Entonces un giro de cualquier ángulo en torno a tal eje hace que las componentes de $\vec{E}$ aunque el plano no ha cambiado para nada. Luego $\vec{E}$ debe ser completamente perpendicular al plano.

Para el caso de un cilindro infinito de densidad de carga uniforme, el argumento funciona de forma similar para un eje cortando en perpendicular al eje del cilindro en cualquiera de sus puntos, esto es, en dirección radial al eje del cilindro. La conclusión es que el vector $\vec{E}$ lleva la dirección radial al eje del cilindro.

Volviendo al plano infinito, para aplicar la Ley de Gauss lo útil es tomar una superficie cerrada que tenga alguna parte paralela al plano: así el vector diferencial $d\vec{S}$ de esta parte será paralelo a $\vec{E}$ y además $\vec{E}$ será constante en todos los puntos de esta parte de la superficie cerrada. Ejemplo de superficie: un cilindro tapado cuyas dos tapas planas sean paralelas al plano cargado

$$\oint_{S={\scriptscriptstyle \rm cilindro tapado}}\hspace{-... ...displaystyle =0}= 2E_\perp S_{\scriptscriptstyle \rm tapa} ,$$

donde $S_{\scriptscriptstyle \rm tapa}$ es el área de cada una de las tapas del cilindro. $E_\perp$ denota que el vector del campo eléctrico es normal al plano, y por ello, el área lateral del cilindro no contribuye a la integral de arriba ya que para el $d\vec{S}$ para el lateral es paralelo al plano y por tanto perpendicular a $\vec{E}$. Ya sólo queda calcular la carga que hay dentro del cilindro tapado: esta carga sólo puede estar en la parte del plano infinito cargado que ``corta'' el cilindro, y la carga que contiene esta parte del plano infinito es $Q_{\scriptscriptstyle \rm dentro}=\sigma S_{\scriptscriptstyle \rm tapa}$. De acuerdo con la Ley de Gauss obtenemos entonces

$$2E_\perp S_{\scriptscriptstyle \rm tapa}=\frac{Q_{\scriptscr... ...ongrightarrow\quad E_\perp = \frac{\sigma}{2\varepsilon_0} .$$ (21)

Es importante notar que este campo no disminuye con la distancia al plano, a diferencia del campo creado por un hilo infinito cargado o el campo creado por una carga puntual.

*Suplemento. Otra forma de obtener (21) es la siguiente: de acuerdo con el resultado (12), el campo creado por un anillo de radio a a una distancia x sobre el eje perpendicular al centro del anillo es igual a ${\displaystyle \frac{1}{4\pi\varepsilon_0} \frac{Qx}{(a^2+x^2)^{3/2}}}$ donde Q es la carga que porta el anillo; la dirección de este campo es perpendicular al plano del anillo. Consideremos que el anillo tiene un grosor infinitesimal da y por tanto un área $2\pi ada$: un plano infinito lo podemos construir sumando estos anillos cuyo radio varíe de $a=0$ hasta $a=\infty$. La carga que lleva cada anillo es $Q=\sigma 2\pi a da$ y el campo creado entonces por un plano infinito es

$$E=\int_{a=0}^{a=\infty}\frac{1}{4\pi\varepsilon_0} \frac{x}{... ...}\frac{da}{(a^2+x^2)^{3/2}} =\frac{\sigma}{2\varepsilon_0} ,$$ (22)

que es el resultado buscado; notar que ${\displaystyle \int \frac{da}{(a^2+x^2)^{3/2}}=-\frac{1}{\sqrt{a^2+x^2}}}$.

En el problema, los dos campos creados por los planos verticales son

$$\begin{array}{ll} \vec{E}_a &\hspace{-2mm}=\hspace{-1mm}\lef... ...on_0} \hat{i}} & x<2{\rm m} , \end{array}\right.\end{array}$$

con $\sigma_a=-3.5\times 10^{-6}{\rm C/m^2}$ y $\sigma_a=6\times 10^{-6}{\rm C/m^2}$. Calcular el campo resultamente se hace ahora directamente

$$\vec{E}_a+\vec{E}_b=\left\{\hspace{-1mm}\begin{array}{ll} {\... ...a_b}{2\varepsilon_0} \hat{i}} & x>2{\rm m}\end{array}\right.$$ (23)

P.14 La carga que hay dentro de una esfera de radio r es

$$Q_{\scriptscriptstyle \rm dentro} =\int_{R=0}^{R=r}\rho 4\pi... ...\rho \frac{4\pi}{3}(b^3-a^3)} & r\geq b ,\end{array}\right.$$

teniendo en cuenta que el volumen de una corteza esférica de de radio R y grosor infinitesimal dR es igual a $4\pi R^2dR$. Puesto que la densidad de carga sólo depende de la distancia radial, la simetría del campo eléctrico es igual a la del problema 10: el campo es radial. 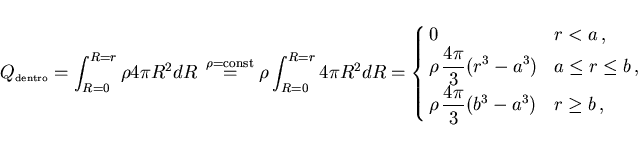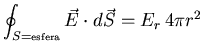Por lo tanto, tomando como superficie cerrada de integración una esfera de radio r, se cumple que ${\displaystyle \oint_{S={\scriptscriptstyle \rm esfera}}\vec{E}\cdot d\vec{S} =E_r 4\pi r^2}$ y la Ley de Gauss aplicada a este caso nos da:

$$E_r=\frac{1}{4\pi r^2}\frac{Q_{\scriptscriptstyle \rm dentro... ...^3-a^3)}{3\varepsilon_0 r^2}} & r\geq b , \end{array}\right.$$ (24)

sustituyendo el valor de la carga que queda dentro de la superficie de radio r sobre la que estamos integrando. El resultado anterior también se puede escribir en función de la carga total ${\displaystyle Q_{\scriptscriptstyle \rm total} =\int_{R=0}^{R=\infty}\rho 4\pi R^2dR=\rho \frac{4\pi}{3}(b^3-a^3)}$

$$E_r=\left\{\begin{array}{ll} 0 & r<a ,\\ {\displaystyle \... ...i\varepsilon_0}\frac{1}{r^2}} & r\geq b , \end{array}\right.$$ (25)

en vez de en función de la densidad de carga.

P.15 Se sigue aplicando que la simetría de $\vec{E}$ es radial y por tanto al integrar sobre una superficie esférica de radio r se obtiene

$$\displaystyle \oint_{S={\scriptscriptstyle \rm esfera}}\vec{... ...Q_{\scriptscriptstyle {\rm dentro de }S}}{\varepsilon_0} .$$

Puesto que la densidad volumétrica de varga sólo depende de la distancia radial (pero no de ningún ángulo), la carga que queda dentro de la esfera de radio r es

$$Q_{\scriptscriptstyle \rm dentro}=\int_{r'=0}^{r'=r}\hspace{... ...space{-1mm}4\pi r'^2dr'=A\pi R^4} & r\geq R \end{array}\right.$$

de donde se obtiene el módulo del campo eléctrico

$$E_r=\frac{1}{4\pi r^2}\frac{Q_{\scriptscriptstyle \rm dentro... ...ac{AR^4}{4\varepsilon_0 r^2}} & r\geq R . \end{array}\right.$$ (26)

O expresado en función de la carga total ${\displaystyle Q_{\scriptscriptstyle \rm total} =\int_{R=0}^{R=\infty}\rho 4\pi R^2dR=A\pi R^4}$

$$E_r=\left\{\begin{array}{ll} {\displaystyle \frac{Q_{\script... ...i\varepsilon_0}\frac{1}{r^2}} & r\geq R . \end{array}\right.$$ (27)

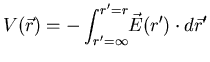El potencial en un punto a una distancia r viene definido por ${\displaystyle V(\vec{r})=-\int_{r'=\infty}^{r'=r}\hspace{-1mm} \vec{E}(r')\cdot d\vec{r}'}$ (ver ecuación (32)) y así para fuera de la esfera, $r\geq R$, tenemos

$$V(r)=-\int_{r'=\infty}^{r'=r}E_r(r')dr'= -\int_{r'=\infty}^{... ...\scriptscriptstyle \rm total}}{4\pi\varepsilon_0} \frac 1r .$$ (28)

Y para dentro de la esfera, o $r<R$,

$$V(r)=-\int_{r'=\infty}^{r'=R}\frac{AR^4}{4\varepsilon_0 r'^2... ...c{AR^3}{4\varepsilon_0}+\frac{A(R^3-r^3)}{12\varepsilon_0} ,$$ (29)

o bien

$$V(r)=\frac{Q_{\scriptscriptstyle \rm total}}{4\pi\varepsilon_0}\frac 1R\left(\frac 43 -\frac{r^3}{3R^3}\right)\quad r<R .$$ (30)

P.16 La línea cargada está fuera de la esfera: el campo eléctrico creado por la esfera de carga uniforme fuera se calcula por la Ley de Gauss integrando sobre una esfera cerrada de radio $r>R$ que contiene completamente toda la carga de la esfera cargada

$$\displaystyle \oint_{S={\scriptscriptstyle \rm esfera}}\vec{... ...m dentro de }S}}{\varepsilon_0} =\frac{Q}{\varepsilon_0} .$$

Por lo tanto, la fuerza que siente un elemento de longitud dr de la línea cargada es ${\displaystyle dF=E_r dq=\frac{Q}{4\pi\varepsilon_0 r^2} \lambda dr}$ donde $\lambda$ es la densidad lineal de carga de la línea. Así

$$F=\int_{r=R}^{r=R+d}\frac{Q}{4\pi\varepsilon_0 r^2} \lambda... ...da}{4\pi\varepsilon_0} \left(\frac 1R-\frac{1}{R+d}\right) .$$ (31)