En la sección anterior hemos estudiado el patrón de difracción producido por una red formada por un número enorme de rendijas paralelas. Cada una de estas rendijas la hemos supuesto muy, muy estrecha de forma que actúe como un foco puntual emisor de frentes de ondas perfectamente cilíndricos (aunque ahora la anchura de la rendija ya no va a ser cero, seguimos considerando que su longitud es infinita).
Pero qué sucede cuando la rendija no es tan estrecha, aunque siempre manteniendo una anchura que no sea excesivamente grande en comparación con la(s) longitud(es) de onda que llega(n) a la rendija (ya que de lo contrario no habría difracción).
Consideremos el caso de una única rendija de anchura a
pequeña pero no despreciable que está iluminada perpendicularmente
por una luz puntual monocromática coherente (por ejemplo, la de un
láser) de longitud de onda ![]() . Esta rendija difracta la luz
en todas las direcciones y nosotros observamos la luz que llega desde
una dirección
. Esta rendija difracta la luz
en todas las direcciones y nosotros observamos la luz que llega desde
una dirección ![]() .
Como ahora la rendija no es tan estrecha, la difracción que provoca,
aunque se sigue propagando en todas las direcciones ya no es con
frentes de onda cilíndricos.
De acuerdo con el Principio de Huygens, suponemos que dentro de la
anchura de la rendija ``caben'' muchos (infinitos) focos emisores
puntuales de frentes de ondas cilíndricos que al superponerse unos
con otros dan como resultado el frente de onda de la luz difractada
por la rendija.
Puesto que la luz que ilumina la rendija es coherente, estos focos
emisores están en fase unos con otros; y, repitiendo, la luz que nos
llegue a un punto determinado será el resultado de la interferencia
entre las ondas emitidas en cada foco contenido dentro del ancho de la
rendija.
Notar que ahora cada uno de los focos puntuales emisores de ondas
cilíndricas no está en diferentes rendijas infinitesimalmente
estrechas (como era el caso de la
red de difracción)
sino dentro de una sola rendija de anchura no despreciable.
.
Como ahora la rendija no es tan estrecha, la difracción que provoca,
aunque se sigue propagando en todas las direcciones ya no es con
frentes de onda cilíndricos.
De acuerdo con el Principio de Huygens, suponemos que dentro de la
anchura de la rendija ``caben'' muchos (infinitos) focos emisores
puntuales de frentes de ondas cilíndricos que al superponerse unos
con otros dan como resultado el frente de onda de la luz difractada
por la rendija.
Puesto que la luz que ilumina la rendija es coherente, estos focos
emisores están en fase unos con otros; y, repitiendo, la luz que nos
llegue a un punto determinado será el resultado de la interferencia
entre las ondas emitidas en cada foco contenido dentro del ancho de la
rendija.
Notar que ahora cada uno de los focos puntuales emisores de ondas
cilíndricas no está en diferentes rendijas infinitesimalmente
estrechas (como era el caso de la
red de difracción)
sino dentro de una sola rendija de anchura no despreciable.
Para facilitar más el estudio de este caso vamos a considerar que el punto donde observamos la imagen está muy alejado de la rendija, para que así podamos considerar que los rayos, que van a parar e interfieren en el punto donde colocamos el ojo o el detector, sean prácticamente paralelos. Tal caso se denomina difracción de Fraunhofer para una rendija.
Como se ve en la figura 3, supongamos
que la dirección ![]() bajo la que llegan los rayos cumple la
condición
bajo la que llegan los rayos cumple la
condición
![]() : en tal caso se ve claramente que el rayo
difractado justo en el borde superior de la rendija interfiere
destructivamente (=está desfasado en media longitud de onda) con el
rayo difractado en la mitad de la rendija; y este rayo a su vez
interfiere destructivamente con el rayo difractado en el borde
inferior de la rendija.
: en tal caso se ve claramente que el rayo
difractado justo en el borde superior de la rendija interfiere
destructivamente (=está desfasado en media longitud de onda) con el
rayo difractado en la mitad de la rendija; y este rayo a su vez
interfiere destructivamente con el rayo difractado en el borde
inferior de la rendija.
En la mayoría de los casos cuando se estudia la difracción de
Fraunhofer, la situación es la representada en la
figura 4, en la que estamos observando
el patrón de interferencia sobre una pantalla muy alejada de la rendija.
El ángulo ![]() , en el que llegan los rayos que van a interferir
en un punto a una distancia y del máximo central, es lo
suficientemente pequeño para poder aproximar su seno por su
tangente, con lo que las posiciones
, en el que llegan los rayos que van a interferir
en un punto a una distancia y del máximo central, es lo
suficientemente pequeño para poder aproximar su seno por su
tangente, con lo que las posiciones ![]() sobre la pantalla para intensidad
nula es, según (3)
sobre la pantalla para intensidad
nula es, según (3)
Importante. Repetimos: no confundir la rendija única de
anchura a, que es lo que estamos viendo, con la
red de difracción,
que está formada por muchísimas rendijas siendo la anchura de
cada rendija prácticamente cero.
Mientras que
![]() (con m entero distinto de
cero) indica los ángulos para intensidad cero en la
difracción de Fraunhofer de una única rendija, la relación
(con m entero distinto de
cero) indica los ángulos para intensidad cero en la
difracción de Fraunhofer de una única rendija, la relación
![]() (con m entero cualquiera) da los
ángulos para máximo en una red de difracción.
(con m entero cualquiera) da los
ángulos para máximo en una red de difracción.
La discusión anterior para la difracción de Fraunhofer en una
única rendija ha sido, aunque correcta, sólo cualitativa: de
hecho, a pesar de saber que dentro de la anchura de la rendija hay
infinitos focos emisores de ondas cilíndricas, para la condición
de interferencia completamente destructiva sólo hemos
considerado tres focos (extremos superior, centro y extremo inferior).
Esto es así ya que lo mismo va a ocurrir con un foco un poco por
debajo del extremo superior y su correspondiente foco desplazado en la
misma distancia por debajo del punto medio.
Aun así la discusión anterior sólo nos ha permitido obtener
los puntos de intensidad cero, y el máximo central para
![]() .
Pero la intensidad para otros ángulos que no sean ni cero ni que
cumplan la condición (3) hay que obtenerla por un
procedimiento más preciso, y su resultado es
.
Pero la intensidad para otros ángulos que no sean ni cero ni que
cumplan la condición (3) hay que obtenerla por un
procedimiento más preciso, y su resultado es
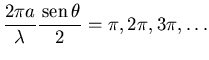 o equivalentemente para
o equivalentemente para
 con lo que
con lo que
Sin embargo, la intensidad no sólo depende del ángulo sino
también de la anchura de la rendija, como se ve en la
figura 6 para tres valores crecientes
de la anchura de la rendija frente a la
longitud de onda de la luz monocromática que ilumina la rendija.
Notar que a medida que aumenta la anchura de la rendija el patrón de
tiende a una única mancha puntual central: el punto que corresponde
a la fuente puntual coherente (por ejemplo, el láser) que iluminaba
la rendija.
Esta propiedad se deriva directamente de la ecuación
(5): salvo para el ángulo ![]() -- que como ya sabemos
corresponde a la máxima intensidad independientemente de la anchura
de la rendija -- el límite de a tendiendo a infinito
produce
-- que como ya sabemos
corresponde a la máxima intensidad independientemente de la anchura
de la rendija -- el límite de a tendiendo a infinito
produce

En clase de teoría ya habrás visto que una manera gráfica de visualizar la interfenrencia de muchas ondas es utilizando fasores. En el fondo estos fasores no es otra cosa que el representar números complejos de módulo unidad. Aunque este sistema es bastante inmediato de entender, aquí vamos a utilizar los números complejos directamente, ya que es más cómodo, rápido y exacto. Por otra parte, los siguientes resultados matemáticos que vas a obtener te pueden ser útiles al sumar funciones trigonométricas.

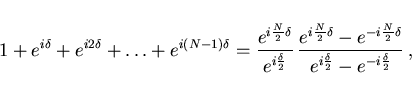
 .
En los siguientes pasos veremos que este último resultado es
precisamente la intensidad de la luz que llega a la pantalla
infinitamente alejada de una rendija en la que cabe un número finito
N de focos emisores coherentes de frentes de onda cilíndricos
.
En los siguientes pasos veremos que este último resultado es
precisamente la intensidad de la luz que llega a la pantalla
infinitamente alejada de una rendija en la que cabe un número finito
N de focos emisores coherentes de frentes de onda cilíndricos
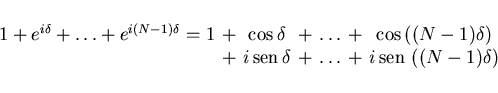
Como se ve en la figura 7, para una
dirección ![]() en la que llegan los rayos paralelos de cada uno
de los focos emisores, el desfase entre dos rayos consecutivos es
en la que llegan los rayos paralelos de cada uno
de los focos emisores, el desfase entre dos rayos consecutivos es
 : así si
tomamos que
: así si
tomamos que
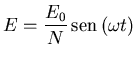 es la onda
difractada por el foco emisor localizado en el primer segmento de
longitud a/N, entonces la onda emitida por el siguiente foco
está descrita por
es la onda
difractada por el foco emisor localizado en el primer segmento de
longitud a/N, entonces la onda emitida por el siguiente foco
está descrita por
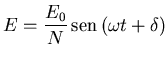 y
así sucesivamente; el significado de
y
así sucesivamente; el significado de ![]() se verá un poco más
adelante.
Notar al aumentar el número de divisiones de la rendija para llegar
finalmente a una distribución continua de focos emisores, el desfase
y la amplitud de cada onda disminuye.
se verá un poco más
adelante.
Notar al aumentar el número de divisiones de la rendija para llegar
finalmente a una distribución continua de focos emisores, el desfase
y la amplitud de cada onda disminuye.
Sobre la pantalla interfieren todas estas ondas que van desfasadas en
![]() una con la siguiente: utilizando la relación
una con la siguiente: utilizando la relación
![]() en las funciones seno que contienen algún desfase, se obtiene que la
onda resultante de tal interferencia viene dada por
en las funciones seno que contienen algún desfase, se obtiene que la
onda resultante de tal interferencia viene dada por

![\begin{displaymath}
\begin{array}{lcl}
E_{\scriptscriptstyle \rm resul}= &&
{\di...
...n}\,\left(\frac\delta 2\right)}\right)
\right]\, ,}
\end{array}\end{displaymath}](img60.png)
En cuanto al significado de ![]() hay que notar que para el caso
hay que notar que para el caso ![]() no
hay desfase (
no
hay desfase (![]() ) entre cada uno de los rayos que llegan en
perpendicular a la pantalla desde cada uno de los focos emisores:
) entre cada uno de los rayos que llegan en
perpendicular a la pantalla desde cada uno de los focos emisores: