DIFRACCIÓN DE FRAUNHOFER EN DOBLE RENDIJA

Para el caso del sistema formado por dos rendijas de anchura a cada una y separadas una distanca d, la extensión de los resultados del caso anterior es directa. Seguimos suponiendo que la distancia a la pantalla es infinita de forma que los rayos difractados por cada rendija son paralelos entre sí (ver figura 8). Para un punto sobre la pantalla donde interfieren estos dos rayos que llegan en una dirección $\theta$, la diferencia de camino entre los dos rayos es ${d\,{\rm sen}\,\theta}$.

Y por lo tanto, si la onda difractada en la primera rendija (de anchura no despreciable) viene dada por (14), entonces la onda difractada en la otra rendija estará desfasada en ${\displaystyle \delta'=\frac{2\pi}{\lambda}d\,{\rm sen}\,\theta}$

$$% latex2html id marker 847\hspace{-0.3cm} \left\{\begin{ar... ...}{2} +\mbox{\boldmath$\delta'$}\right)\, .} \end{array}\right.$$ (16)

Puesto que ${\,{\rm sen}\,(\alpha\pm\beta) =\,{\rm sen}\,\alpha\,\cos\beta\pm\cos\alpha\,\,{\rm sen}\,\beta}$ entonces ${\,{\rm sen}\,(\alpha+\beta)+\,{\rm sen}\,(\alpha-\beta)=}$ ${\displaystyle =2\cos\beta\,{\rm sen}\,\alpha}$; y aplicando este resultado con

$$\hspace{-1cm} \left.\begin{array}{lcl} \alpha+\beta &\hspace... ...{\lambda}\frac{\,{\rm sen}\,\theta}{2}}\, . \end{array}\right.$$

a la suma de las dos ondas en (16) se obtiene inmediatamente que la onda sobre la pantalla muy alejada resultante de la interferencia entre los dos rayos difractados en la doble rendija es

$$\hspace{-0.4cm} \underline{2 E_0\left(\frac{\displaystyle \,... ...c{2\pi (a+d)}{\lambda}\frac{\,{\rm sen}\,\theta}{2}\right)\, .$$ (17)

La amplitud es la parte subrayada y la intensidad sobre la pantalla se obtiene de elevar al cuadrado esta parte subrayada

$$I_{\scriptscriptstyle \rm doble\:ren.}(\theta)=4I_0 \left(\f... ...frac{2\pi d}{\lambda}\frac{\,{\rm sen}\,\theta}{2}\right) \, .$$ (18)

La representación de la intensidad sobre la pantalla para ángulos muy pequeños, tal que ${\,{\rm sen}\,\theta\approx y/L}$ se puede ver en la figura 9 para el caso L=4 m, $a/\lambda=200$ y $d/\lambda=400$. Darse cuenta del factor 4 en la intensidad ya que ahora al tener dos rendijas, a cada una le corresponde una amplitud de máximo central igual a $E_0$ y por tanto el máximo central resultante tendrá una amplitud de $2E_0$ y una intensidad de ${(2E_0)^2=4I_0}$.

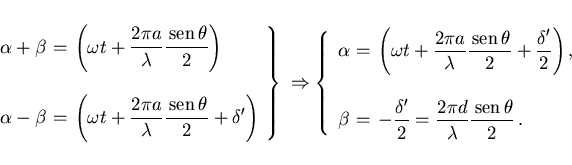
Es importante notar que para una única rendija los máximos de intensidad sobre la pantalla tienen un ancho más grande que para el montaje experimental con dos rendijas de las mismas dimensiones: comparar la figura 6 para una rendija con la figura 9 para la doble rendija y ver como el máximo central para el primer caso ocupa el espacio sobre la pantalla en el que para la doble rendija cabe el máximo central y un máximos secundarios más a cada lado. Notar además que la distribución de los máximos para la doble rendija quedan ``envueltos'' (=modulados) por la curva correspondiente a la intensidad de la única rendija.

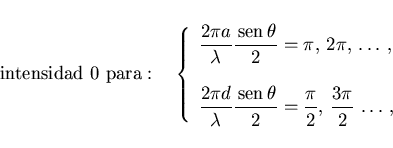
La posición de los mínimos de intensidad cero corresponden a cuando (18) sea cero:

$$\mbox{intensidad 0 para}:\quad\left\{ \begin{array}{l} {\dis... ...}=\frac\pi 2,\,\frac{3\pi}{2}\, \ldots\, ,} \end{array}\right.$$

o bien

$$\mbox{intensidad 0 para}:\quad\left\{ \begin{array}{l} a\,{\... ...\lambda 2,\,\frac{3\lambda}{2}\,\ldots\, .} \end{array}\right.$$ (19)