

Up: Prácticas de Física para I.T.I. & I.T.A.
Previous: Concepto de derivada
EL MOVIMIENTO ARMÓNICO SIMPLE
Para una variable que depende del tiempo, x(t), el movimiento armónico simple se define como aquel en que la segunda derivada de la variable es proporcional a menos la variable sin derivar.
Esto expresado matemáticamente toma la forma de
 |
(1) |
La constante de proporcionalidad entre la segunda derivada de la variable y menos la variable sin derivar es positiva y se escribe como 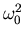 ; a
; a  se le llama la frecuencia natural del movimiento armónico simple y es una constante.
El porqué de este nombre de ``frecuencia natural'' deriva de lo siguiente: una manera sencilla de imaginar un movimiento armónico simple es como proyección de perfil de un movimiento circular uniforme.
Supongamos que tenemos un disco de radio R sobre una mesa con un pequeño pivote rojo vertical pegado al borde, y que al disco le damos un movimiento circular con velocidad (o frecuencia) constante
se le llama la frecuencia natural del movimiento armónico simple y es una constante.
El porqué de este nombre de ``frecuencia natural'' deriva de lo siguiente: una manera sencilla de imaginar un movimiento armónico simple es como proyección de perfil de un movimiento circular uniforme.
Supongamos que tenemos un disco de radio R sobre una mesa con un pequeño pivote rojo vertical pegado al borde, y que al disco le damos un movimiento circular con velocidad (o frecuencia) constante 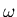 .
Si ahora ponemos la vista a la altura de la mesa de forma que veamos el disco de perfil, el movimiento que le observamos al pivote rojo es exactamente un movimiento (oscilatorio) armónico simple; oscilatorio porque se repite exactamente a lo largo del tiempo.
Esto es lo que se ve en la figura 1.
El ángulo que se ha desplazado el pivote desde la posición de partida viene dado por
.
Si ahora ponemos la vista a la altura de la mesa de forma que veamos el disco de perfil, el movimiento que le observamos al pivote rojo es exactamente un movimiento (oscilatorio) armónico simple; oscilatorio porque se repite exactamente a lo largo del tiempo.
Esto es lo que se ve en la figura 1.
El ángulo que se ha desplazado el pivote desde la posición de partida viene dado por
 ya que el pivote (visto desde arriba) describe un movimiento circular uniforme.
Y por tanto, la ecuación para el desplazamiento x(t) que se observa de perfil se obtiene con un cálculo de trigonometría sencillo
ya que el pivote (visto desde arriba) describe un movimiento circular uniforme.
Y por tanto, la ecuación para el desplazamiento x(t) que se observa de perfil se obtiene con un cálculo de trigonometría sencillo
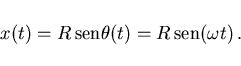 |
(2) |
Que esta ecuación corresponde a la ecuación (1) que define un movimiento armónico simple se obtiene inmediatamente derivando
 |
(3) |
si la frecuencia natural  del movimiento armónico simple se identifica con la frecuencia (o velocidad) de rotación
del movimiento armónico simple se identifica con la frecuencia (o velocidad) de rotación 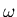 constante del movimiento circular uniforme.
La solución
constante del movimiento circular uniforme.
La solución
 |
(4) |
es igualmente solución para el movimiento armónico simple, tal y como se ve en la figura 2, con sólo considerar que el comienzo del movimiento es cuando el pivote rojo está en la parte más a la izquierda de su recorrido.
Es importante volver a destacar que la frecuencia natural del movimiento armónico coincide con la velocidad angular del movimiento circular -- del que el movimiento armónico simple es su proyección de perfil -- sólo si el movimiento circular es uniforme, es decir, si no está acelerado.
Ahora vamos a considerar el movimiento de un péndulo simple, para saber bajo qué condiciones se le puede considerar un movimiento armónico simple.
Un péndulo simple está formado por un cuerpo de masa m que se puede considerar puntual sujeto por un hilo de masa despreciable y longitud R.
Cuando esta masa se separa un ángulo  de la vertical, el péndulo realiza un movimiento oscilatorio bajo la acción de la gravedad g.
Su esquema está representado en la figura 3.
de la vertical, el péndulo realiza un movimiento oscilatorio bajo la acción de la gravedad g.
Su esquema está representado en la figura 3.
Es claro que el movimiento del péndulo, aunque circular, ya no es con velocidad angular constante: en el punto más bajo de la trayectoria la velocidad angular es la mayor posible, mientras que para los puntos más altos de la trayectoria, cuando
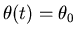 , la velocidad angular es cero.
Luego ya no podemos identificar la frecuencia natural
, la velocidad angular es cero.
Luego ya no podemos identificar la frecuencia natural  del movimiento armónico simple (caso de que el movimiento del péndulo sea armónico simple), que es una constante, con la velocidad angular del movimiento circular que realiza la masa m.
del movimiento armónico simple (caso de que el movimiento del péndulo sea armónico simple), que es una constante, con la velocidad angular del movimiento circular que realiza la masa m.
Veamos cuál es la ecuación que describe el movimiento del péndulo.
En vez de resolverlo planteando qué fuerzas son las que actuán sobre la masa m (tal y como viene en la página 382 del libro de Física de P. A. Tipler), lo vamos a plantear a través de la conservación de la energía mecánica.
El uso de tal conservación de la energía viene justificado porque la fuerza de la gravedad es una fuerza conservativa y la tensión del hilo no realiza trabajo ya que el desplazamiento de la masa m tiene lugar siempre de forma perpendicular a la tensión.
La velocidad lineal de la masa m es igual al radio R, del arco de circunferencia que describe, multiplicado por la velocidad angular
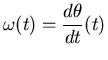 ; mientras que la altura h que corresponde a cuando la masa m está separada un ángulo
; mientras que la altura h que corresponde a cuando la masa m está separada un ángulo 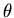 de la vertical viene dada por
de la vertical viene dada por
 como se puede despejar de forma sencilla de la figura 3.
Por tanto la energía mecánica del péndulo simple, suma de la energía cinética más la energía potencial gravitatoria es igual a
como se puede despejar de forma sencilla de la figura 3.
Por tanto la energía mecánica del péndulo simple, suma de la energía cinética más la energía potencial gravitatoria es igual a
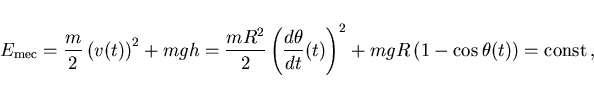 |
(5) |
que es una constante a lo largo del tiempo (si se desprecia el rozamiento con el aire).
Y por ser una constante su derivada con respecto al tiempo es cero,
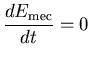 , luego también se cumple
, luego también se cumple
![\begin{displaymath}
\frac{d}{dt}\left[\frac{mR^2}{2}\left(\frac{d\theta}{dt}(t)\right)^2
+mgR\left(1-\cos\theta(t)\right)\right]=0\, .
\end{displaymath}](img19.png) |
(6) |
Ya sólo queda desarrollar esta derivada para obtener la ecuación del péndulo simple
y sustituyendo en (6)
y operando un poco se obtiene
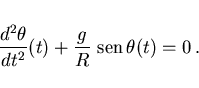 |
(7) |
Esta claro que esta ecuación (7) no es igual a la ecuación de un movimiento armónico simple, la cual según su definición (1), debería haber sido
 : hay que notar que en (7) aparece el seno del ángulo, no el ángulo simplemente.
Luego en general, el movimiento de un péndulo simple no es un movimiento armónico simple.
: hay que notar que en (7) aparece el seno del ángulo, no el ángulo simplemente.
Luego en general, el movimiento de un péndulo simple no es un movimiento armónico simple.
Sin embargo, para oscilaciones pequeñas, el seno del ángulo (medido en radianes) se puede aproximar por el ángulo mismo,
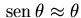 , y entonces (7) toma la forma
, y entonces (7) toma la forma
 |
(8) |
que sí es la ecuación de un movimiento armónico simple, con frecuencia natural  igual a
igual a
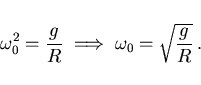 |
(9) |
Para terminar, se define el periodo como
 , que en el caso de un péndulo simple realizando oscilaciones pequeñas es igual a
, que en el caso de un péndulo simple realizando oscilaciones pequeñas es igual a
 |
(10) |



Up: Prácticas de Física para I.T.I. & I.T.A.
Previous: Concepto de derivada
José Luis Marqués 01.12.01

![]() de la vertical, el péndulo realiza un movimiento oscilatorio bajo la acción de la gravedad g.
Su esquema está representado en la figura 3.
de la vertical, el péndulo realiza un movimiento oscilatorio bajo la acción de la gravedad g.
Su esquema está representado en la figura 3.
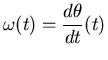 ; mientras que la altura h que corresponde a cuando la masa m está separada un ángulo
; mientras que la altura h que corresponde a cuando la masa m está separada un ángulo ![]() de la vertical viene dada por
de la vertical viene dada por
![]() como se puede despejar de forma sencilla de la figura 3.
Por tanto la energía mecánica del péndulo simple, suma de la energía cinética más la energía potencial gravitatoria es igual a
como se puede despejar de forma sencilla de la figura 3.
Por tanto la energía mecánica del péndulo simple, suma de la energía cinética más la energía potencial gravitatoria es igual a
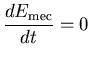 , luego también se cumple
, luego también se cumple
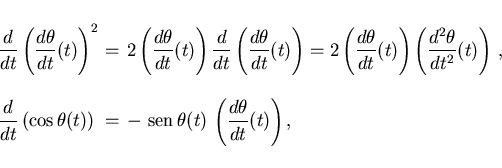
![\begin{displaymath}
\left(\frac{d\theta}{dt}(t)\right)\left[\frac{2mR^2}{2}
\frac{d^2\theta}{dt^2}(t)+mgR\,\,{\rm sen}\,\/\theta(t)\right]=0\, ,
\end{displaymath}](img21.png)
 : hay que notar que en (7) aparece el seno del ángulo, no el ángulo simplemente.
Luego en general, el movimiento de un péndulo simple no es un movimiento armónico simple.
: hay que notar que en (7) aparece el seno del ángulo, no el ángulo simplemente.
Luego en general, el movimiento de un péndulo simple no es un movimiento armónico simple.
![]() , y entonces (7) toma la forma
, y entonces (7) toma la forma
 , que en el caso de un péndulo simple realizando oscilaciones pequeñas es igual a
, que en el caso de un péndulo simple realizando oscilaciones pequeñas es igual a