

Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
Los datos que hay que representar son:
 |
-1 |
-0.921 |
-0.854 |
-0.796 |
-0.745 |
-0.699 |
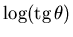 |
0.312 |
0.092 |
-0.123 |
-0.293 |
-0.493 |
-0.572 |
 |
-0.658 |
-0.620 |
-0.585 |
-0.553 |
-0.523 |
|
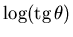 |
-0.711 |
-0.800 |
-0.911 |
-1.058 |
-1.155 |
|
cuya representación se puede ver en la siguiente figura.
De acuerdo con la hipótesis, la pendiente de la recta del
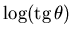 frente al
frente al 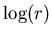 es el número entero
-n.
Puesto que una vez representados estos puntos vemos que están
aproximadamente sobre una recta y
además la pendiente debe ser un número entero (con lo que no hace
flata gran exactitud a la hora de calcular la pendiente), podemos
hallar esta pendiente sencillamente tomando dos parejas cualesquiera
de valores, por ejemplo, las dos primeras parejas de valores
es el número entero
-n.
Puesto que una vez representados estos puntos vemos que están
aproximadamente sobre una recta y
además la pendiente debe ser un número entero (con lo que no hace
flata gran exactitud a la hora de calcular la pendiente), podemos
hallar esta pendiente sencillamente tomando dos parejas cualesquiera
de valores, por ejemplo, las dos primeras parejas de valores
 |
(6) |
Otra forma de hallar la pendiente es de forma gráfica: después de
dibujar todos los puntos correspondientes a las medidas, se traza a
``ojo'' y con una regla la recta que pase lo más próximo posible a
todos los puntos.
La pendiente de dicha recta se obtiene midiendo el ángulo que forma
dicha recta con la horizontal: la pendiente será la tangente
trigonométrica de dicho ángulo, si es que se ha utilizado la misma
escala en el eje vertical y en el eje horizontal, o bien, la pendiente
será dicho número multiplicado por k si es que la
separación entre puntos del eje vertical es k-veces más
grnade que la del eje horizontal.
Como antes, el valor de n será el número entero más
próximo al valor absoluto de la pendiente.
Por otra parte sabemos que
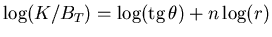 .
Tomando el valor de
.
Tomando el valor de
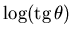 correspondiente a uno
de los valores de
correspondiente a uno
de los valores de 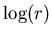 cualquiera, por ejemplo el valor donde
la gráfica anterior corta al eje vertical para
cualquiera, por ejemplo el valor donde
la gráfica anterior corta al eje vertical para 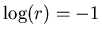 (r=0.1),
y puesto que ya tenemos el valor de n, despejamos inmediatamente:
(r=0.1),
y puesto que ya tenemos el valor de n, despejamos inmediatamente:
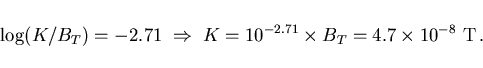 |
(7) |
Suponiendo que podemos aproximar el imán por un dipolo 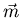 de
dimensiones despreciables y ya que para este experimento el vector
de
dimensiones despreciables y ya que para este experimento el vector
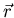 y el vector
y el vector 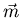 son paralelos, entonces tenemos
son paralelos, entonces tenemos
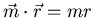 y así:
y así:
El módulo del campo magnético creado por el imán es por tanto
igual a
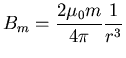 y comparando
este resultado con la hipótesis del comienzo
y comparando
este resultado con la hipótesis del comienzo
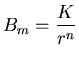 vemos que n es 3, como ya hemos obtenido.
Como
vemos que n es 3, como ya hemos obtenido.
Como
 , el momento dipolar m
es igual a
, el momento dipolar m
es igual a
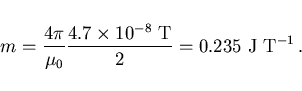 |
(8) |


Next: Soluciones completas en formato
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: Problema 2
José Luis Marqués 15.02.02
![]() .
Tomando el valor de
.
Tomando el valor de
![]() correspondiente a uno
de los valores de
correspondiente a uno
de los valores de ![]() cualquiera, por ejemplo el valor donde
la gráfica anterior corta al eje vertical para
cualquiera, por ejemplo el valor donde
la gráfica anterior corta al eje vertical para ![]() (r=0.1),
y puesto que ya tenemos el valor de n, despejamos inmediatamente:
(r=0.1),
y puesto que ya tenemos el valor de n, despejamos inmediatamente:
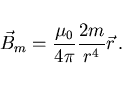
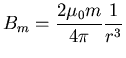 y comparando
este resultado con la hipótesis del comienzo
y comparando
este resultado con la hipótesis del comienzo
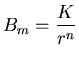 vemos que n es 3, como ya hemos obtenido.
Como
vemos que n es 3, como ya hemos obtenido.
Como
 , el momento dipolar m
es igual a
, el momento dipolar m
es igual a