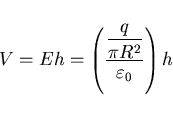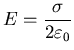 , donde
, donde 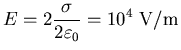 .
Con esto, el valor de la densidad superficial de carga que crea este
campo es igual a
.
Con esto, el valor de la densidad superficial de carga que crea este
campo es igual a
Puesto que el diámetro de la nube, que es igual a 10 km, es un orden
de magnitud mayor que la separación entre la nube y la superficie
terrestre (y la superficie terrestre se puede considerar
prácticamente infinita en extensión), se puede aproximar el
sistema tierra+nube a un condensador plano de placas paralelas.
En tal condensador, el campo electrostático creado por cada una de
las placas es igual a (utilizando el teorema de Gauss)
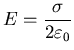 , donde
, donde ![]() es la densidad
superficial de carga; suponemos que el aire entre la nube y la tierra
funciona como si fuera el vacío.
La tierra crea dicho campo apuntando hacia arriba en el espacio entre
la tierra y la nube, y la base de la nube (cargada negativamente) crea
este mismo campo y en la misma direccióny sentido para el espacio
entre ella y la tierra.
Por tanto el campo electrostático que hay entre la tierra y la nube
es igual a
es la densidad
superficial de carga; suponemos que el aire entre la nube y la tierra
funciona como si fuera el vacío.
La tierra crea dicho campo apuntando hacia arriba en el espacio entre
la tierra y la nube, y la base de la nube (cargada negativamente) crea
este mismo campo y en la misma direccióny sentido para el espacio
entre ella y la tierra.
Por tanto el campo electrostático que hay entre la tierra y la nube
es igual a
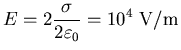 .
Con esto, el valor de la densidad superficial de carga que crea este
campo es igual a
.
Con esto, el valor de la densidad superficial de carga que crea este
campo es igual a
![]() .
La carga almacenada en la base de la nube, que es una superficie
circular de radio R=5 km, es igual a
.
La carga almacenada en la base de la nube, que es una superficie
circular de radio R=5 km, es igual a
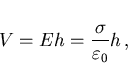
Cuando se produce la descarga eléctrica, y suponiendo que la tierra
y la nube se vacían completamente de carga eléctrica, toda la
energía electrostática almacenada en el condensador se disipa en
forma de calor (rayo y trueno).
Esta energía secalcula de la siguiente forma: consideremos el
condensador tierra+nuba a medio cargar conteniendo una carga q:
la diferencia de potencial entre sus placas es igual a