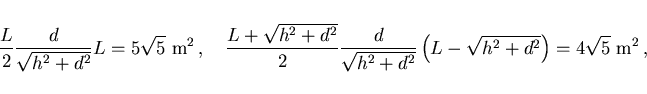

Next: Problema 2
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: SOLUCIONES DE LOS PROBLEMAS
Llamemos L a la longitud del tablón (L=5 m).
Para recoger el papiro del agua, Demetrio tiene que estar sobre la
vertical del rollo de papiro.
La mayor masa posible de Demetrio será aquella para la que, estando
él sobre la vertical del papiro, sus pies rozan el agua: en esta
condición límite, una longitud
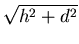 del
tablón está fuera del agua mientras que
del
tablón está fuera del agua mientras que
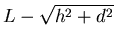 del tablón está sumergido; para estas mismas condiciones, el seno
del ángulo
del tablón está sumergido; para estas mismas condiciones, el seno
del ángulo 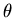 que forma el muelle del puerto con el tablón
es igual a
que forma el muelle del puerto con el tablón
es igual a
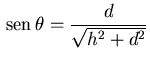 .
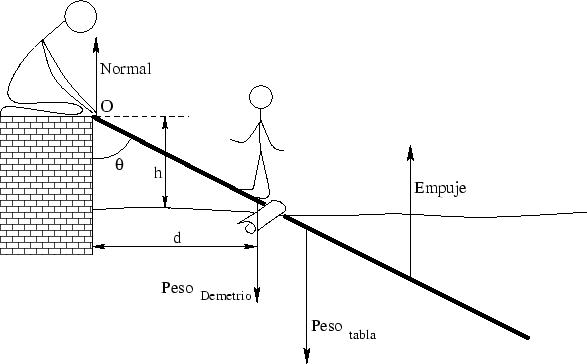
Cuando Demetrio está quieto en esta condición límite, las
únicas fuerzas que actuúan sobre el sistema tablón+Demetrio son
(ver figura):
.
Cuando Demetrio está quieto en esta condición límite, las
únicas fuerzas que actuúan sobre el sistema tablón+Demetrio son
(ver figura):
- El peso de Demetrio
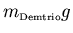 , aplicado a una
distancia d en perpendicular desde el muelle del puerto.
, aplicado a una
distancia d en perpendicular desde el muelle del puerto.
- El peso del tabón
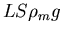 (donde S=8 cm x 65 cm
es la sección del tablón) aplicado a una distancia
(donde S=8 cm x 65 cm
es la sección del tablón) aplicado a una distancia
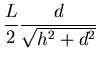 en perpendicular desde el
muelle.
en perpendicular desde el
muelle.
- El empuje hacia arriba de la parte del tablón sumergida
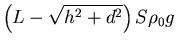 , que está aplicado en
el centro de la parte sumergida, parte que está localizada a una
distancia en perpendicular desde el muelle igual a
, que está aplicado en
el centro de la parte sumergida, parte que está localizada a una
distancia en perpendicular desde el muelle igual a
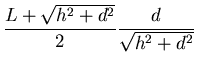 .
.
- La normal hacia arriba aplicada en el punto O que equilibra
junto con el empuje los pesos del tablón y de Demetrio.
En la condición de equilibrio no sólo se debe cumplir que la suma
de fuerzas sea cero, sino que la suma de momentos con respecto a
cualquier punto sea cero.
La suma de los anteriores momentos medidos desde el punto O e igualada
a cero da la siguiente ecuación para la condición límite:
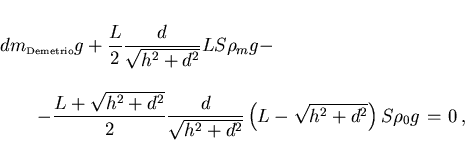 |
(1) |
en donde todo es conocido salvo la masa de Demetrio.
Substituyendo los datos del problema,
se obtiene que la masa máxima de Demetrio es:
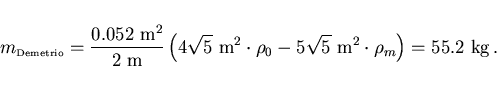 |
(2) |
En el punto en el que Demetrio se queda quieto, para tener el sistema
Demetrio+tablón en equilibrio sólo es necesaria la normal hacia
arriba que hace el muelle del puerto; por tanto en ese momento no es
necesario sujetar el tablón.
Sin embargo, cuando Demetrio se mueve sobre el tablón, la fuerza que
impulsa a Demetrio es la fuerza de rozamiento entre el tablón y
Demetrio: esta fuerza tiene el sentido del movimiento de Demetrio.
La misma fuerza pero en sentido contrario actúa sobre el tablón, y
aunque su componente vertical sea equilibrada por la normal, su
componente horizontal debe ser equilibrada por Arquímedes
sujetando el tablón: tirando hacia sí cuando Demetrio suba o
empujando hacia el mar cuando Demetrio baje.


Next: Problema 2
Up: SOLUCIONES DE LOS PROBLEMAS
Previous: SOLUCIONES DE LOS PROBLEMAS
José Luis Marqués 15.02.02
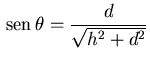 .
Cuando Demetrio está quieto en esta condición límite, las
únicas fuerzas que actuúan sobre el sistema tablón+Demetrio son
(ver figura):
.
Cuando Demetrio está quieto en esta condición límite, las
únicas fuerzas que actuúan sobre el sistema tablón+Demetrio son
(ver figura):
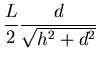 en perpendicular desde el
muelle.
en perpendicular desde el
muelle.
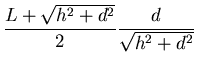 .
.