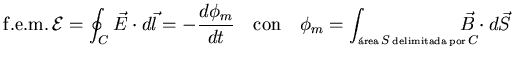
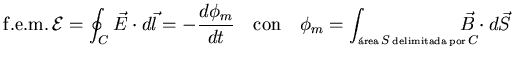
P.41
Un solenoide de sección circular infinitamente largo crea en su
interior un campo magnético uniforme igual a ![]() , donde
n es el número de vueltas que tiene el solenoide por unidad de
longitud; la dirección de este campo es paralelo al eje del
solenoide.
Fuera del solenoide infinito, el campo magnético es cero.
, donde
n es el número de vueltas que tiene el solenoide por unidad de
longitud; la dirección de este campo es paralelo al eje del
solenoide.
Fuera del solenoide infinito, el campo magnético es cero.
Ahora consideremos una bobina formada por N espiras y cuyo radio
![]() es mayor que el radio
es mayor que el radio ![]() de cada espira del solenoide: puesto
que el campo magnético fuera del solenoide es cero,
el único flujo que atraviesa a cada una de las N espiras de la
bobina es igual a
de cada espira del solenoide: puesto
que el campo magnético fuera del solenoide es cero,
el único flujo que atraviesa a cada una de las N espiras de la
bobina es igual a
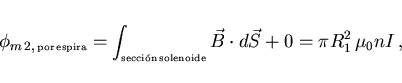
P.42
De acuerdo con la Ley de Faraday un flujo ![]() del campo magnético que
varía con el tiempo al atravesar el área delimitada por un
conductor cerrado produce en este conductor una corriente inducida
igual a
del campo magnético que
varía con el tiempo al atravesar el área delimitada por un
conductor cerrado produce en este conductor una corriente inducida
igual a
 , la integral de la corriente con respecto al
tiempo.
Luego aplicando (3) se obtiene
, la integral de la corriente con respecto al
tiempo.
Luego aplicando (3) se obtiene
P.43
Inicialmente para t=0, el flujo que atraviesa cada una de las
N espiras de superficie ab es máximo ya que cada espira
está completamente perpendicular al campo magnético: cada espira
presenta la mayor superficie posible a ser atravesada por el campo
B, o lo que es lo mismo, el vector superficie (que es normal a
la espira) es paralelo al vector campo magnético.
Al cabo de un cierto tiempo t, la espira ha rotado un ángulo
![]() y por tanto presenta una superficie más pequeña al
campo magnético, siendo este factor de disminución el coseno del
ángulo que forma B con el vector superficie de la espira.
Este coseno es precisamente el que entra en el producto escalar que
define el flujo magnético
y por tanto presenta una superficie más pequeña al
campo magnético, siendo este factor de disminución el coseno del
ángulo que forma B con el vector superficie de la espira.
Este coseno es precisamente el que entra en el producto escalar que
define el flujo magnético
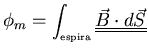 que atraviesa la espira.
El flujo de una campo magnético constante que atraviesa las N
espiras es entonces
que atraviesa la espira.
El flujo de una campo magnético constante que atraviesa las N
espiras es entonces

P.44
Este problema sirve de aplicación del resultado obtenido en el
problema 42.
Si cada espira de radio r=0.01m de una bobina de
N=100 vueltas es atravesada por un campo magnético constante
B=1.0T, entonces el flujo inicial que atraviesa cada espira es
![]() y cuando el campo magnético ha cambiado
de sentido, el flujo es
y cuando el campo magnético ha cambiado
de sentido, el flujo es
![]() .
De auerdo con (4), la carga que ha circulado por toda la
bobina de resistencia R=50 ohmios es
.
De auerdo con (4), la carga que ha circulado por toda la
bobina de resistencia R=50 ohmios es
P.45
El campo magnético creado por un solenoide muy largo (es decir,
que se pueda aproximar a un solenoide infinitamente largo) es igual
a la constante
![]() para cualquier punto en el
interior del solenoide, y cero fuera del solenoide.
La dirección de este campo magnético es paralela al eje del
solenoide.
El flujo magnético que atraviesa una circunferencia de radio r
colocada perpendicularmente al eje del solenoide será entonces
para cualquier punto en el
interior del solenoide, y cero fuera del solenoide.
La dirección de este campo magnético es paralela al eje del
solenoide.
El flujo magnético que atraviesa una circunferencia de radio r
colocada perpendicularmente al eje del solenoide será entonces
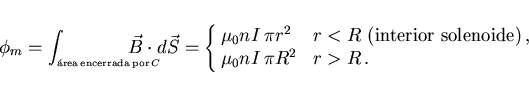


P.46
La posición de la barra,
![]() con
con
![]() y
y
![]() , cambia con el tiempo a lo largo
del eje X, llevando una velocidad
, cambia con el tiempo a lo largo
del eje X, llevando una velocidad
 .
Puesto que este movimiento lo hace dentro de un campo magnético
perpendicular a la velocidad, y puesto que la barra es conductora y
por tanto su carga puede moverse dentro de ella, entonces sobre las
cargas de la barra aparece una fuerza (la fuerza de Lorentz) que es
perpendicular tanto al campo magnético como a la velocidad, es
decir, una fuerza paralela a la barra.
Esta fuerza
.
Puesto que este movimiento lo hace dentro de un campo magnético
perpendicular a la velocidad, y puesto que la barra es conductora y
por tanto su carga puede moverse dentro de ella, entonces sobre las
cargas de la barra aparece una fuerza (la fuerza de Lorentz) que es
perpendicular tanto al campo magnético como a la velocidad, es
decir, una fuerza paralela a la barra.
Esta fuerza ![]() va a mover las cargas libres positivas del conductor hacia
uno de los extermos del conductor (y las cargas negativas hacia el
extremo contrario) creando una acumulación de cargas en los extremos que
crea un campo eléctrico que se opone a la fuerza de Lorentz: la
fuerza de Lorentz seguirá moviendo las cargas libres hasta el
momento en que el campo eléctrico que crean estas cargas desplazadas
compense la fuerza de Lorentz.
Este campo eléctrico de equilibrio tendrá por tanto un módulo
igual a
va a mover las cargas libres positivas del conductor hacia
uno de los extermos del conductor (y las cargas negativas hacia el
extremo contrario) creando una acumulación de cargas en los extremos que
crea un campo eléctrico que se opone a la fuerza de Lorentz: la
fuerza de Lorentz seguirá moviendo las cargas libres hasta el
momento en que el campo eléctrico que crean estas cargas desplazadas
compense la fuerza de Lorentz.
Este campo eléctrico de equilibrio tendrá por tanto un módulo
igual a
![]() ; si la barra se mueve en el sentido del
eje X positivo, el sentido de la fuerza de Lorentz es del eje
Y negativo y por tanto el sentido del campo eléctrico
creado por las cargas desplazadas es el del eje Y positivo.
La diferencia de potencial
; si la barra se mueve en el sentido del
eje X positivo, el sentido de la fuerza de Lorentz es del eje
Y negativo y por tanto el sentido del campo eléctrico
creado por las cargas desplazadas es el del eje Y positivo.
La diferencia de potencial
![]() entre los extremos
de la barra viene dada por
entre los extremos
de la barra viene dada por
Otra forma de obtener este resultado es la siguiente: cuanco la barra
se ha desplazado a lo largo del eje X una distancia
![]() , el flujo del campo magnético que
atraviesa el área barrida por la barra al moverse es
, el flujo del campo magnético que
atraviesa el área barrida por la barra al moverse es
![]() y por tanto, la diferencia de potencial inducida es
y por tanto, la diferencia de potencial inducida es
P.47 En este problema hay que considerar tres intervalos de tiempos:
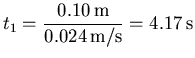 , en
que la espira está entrando dentro de la zona donde hay campo magnético.
, en
que la espira está entrando dentro de la zona donde hay campo magnético.
 en que la
espira recorre el área con campo magnético hasta que su extremo delantero
va a empezar a salir.
en que la
espira recorre el área con campo magnético hasta que su extremo delantero
va a empezar a salir.
 en que la espira sale totalmente de la zona con campo
magnético.
en que la espira sale totalmente de la zona con campo
magnético.

P.49
La corriente en el circuito de la izquierda circula en sentido horario,
del polo positivo al polo negativo de la batería.
Esta corriente crea un campo magnético que va hacia fuera de la
página en los puntos dentro de la superficie delimitada por la
espira derecha.
Si ahora la corriente de la izquierda disminuye repentinamente,
disminuye también el campo magnético que atraviesa la espira derecha.
Como respuesta, en la espira derecha se induce una corriente que al
circular por tal espira intenta reponer el número de líneas de
campo magnético que han disminuido, esto es, la corriente inducida
en la derecha irá en sentido antihorario, porque es en este sentido
que el campo creado por una espira en su centro va hacia fuera de la página.
P.50
El campo creado por un conductor rectilíneo infinito a
una distancia en perpendicular r es igual a
 con dirección circulando alrededor
del conductor y siendo I la corriente que circula
por el conductor: esto se obtiene o bien por integración directa de
la Ley de Biot-Savart o bien aplicando la Ley de Ampére sobre un
camino circular entorno al conductor.
Por tanto, la fuerza que actúa sobre una carga móvil q que
se mueve con una velocidad v paralela al conductor infinito a
una distancia r es
con dirección circulando alrededor
del conductor y siendo I la corriente que circula
por el conductor: esto se obtiene o bien por integración directa de
la Ley de Biot-Savart o bien aplicando la Ley de Ampére sobre un
camino circular entorno al conductor.
Por tanto, la fuerza que actúa sobre una carga móvil q que
se mueve con una velocidad v paralela al conductor infinito a
una distancia r es

 que compensa la fuerza de Lorentz, y
así, tal campo lleva dirección horizontal hacia la derecha (en
el sentido en que crece la distancia r).
La diferencia de potencial, debida al campo E, que aparece entre
los extremos de la varilla móvil es
que compensa la fuerza de Lorentz, y
así, tal campo lleva dirección horizontal hacia la derecha (en
el sentido en que crece la distancia r).
La diferencia de potencial, debida al campo E, que aparece entre
los extremos de la varilla móvil es
P.52 y P.53
El campo creado por el conductor rectilíneo infinito a una
distancia en perpendicular x es igual a
 entrando hacia dentro de la página
para los puntos de la espira de dimensionesaxb, con a=0.05m y b=0.1m.
Consideremos en la espira derecha una tira vertical situada a una
distancia x del conductor rectilíneo, tira de anchura
dx y altura b: el flujo que atraviesa esta tira es
entrando hacia dentro de la página
para los puntos de la espira de dimensionesaxb, con a=0.05m y b=0.1m.
Consideremos en la espira derecha una tira vertical situada a una
distancia x del conductor rectilíneo, tira de anchura
dx y altura b: el flujo que atraviesa esta tira es

Para el problema 53, la distancia d a la que está el lado izquierdo de
la espira crece linealmente con el tiempo ya que la velocidad v con la
que se aleja es constante.
Luego basta con sustituir en la ecuación (13) d por
d+vt

Ahora vamos a obtener el resultado (14) pero calculando
directamente la f.e.m. inducida en cada uno de los segmentos de la
espira rectangular: la técnica es la del
problema 50.
Empecemos por el segmento vertical más próximo al conductor
infinito, conductor que crea un campo magnético
 hacia adentro en los puntos del
segmento.
Puesto que las cargas de este segmento conductor se mueven hacia la
derecha con velocidad v, sobre ellas actúa una fuerza de
Lorentz
hacia adentro en los puntos del
segmento.
Puesto que las cargas de este segmento conductor se mueven hacia la
derecha con velocidad v, sobre ellas actúa una fuerza de
Lorentz
 hacia
arriba, que al desplazar a las cargas termina creando un campo
eléctrico
hacia
arriba, que al desplazar a las cargas termina creando un campo
eléctrico
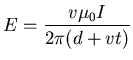 a lo largo del
segmento hacia abajo.
Tomemos un vector
a lo largo del
segmento hacia abajo.
Tomemos un vector ![]() tangente a la espira rectangular y
dirigido en sentido horario: en el segmento vertical que
estamos considerando,
tangente a la espira rectangular y
dirigido en sentido horario: en el segmento vertical que
estamos considerando, ![]() va hacia arriba y por tanto
va hacia arriba y por tanto

 , nos da
, nos da


P.56
Una carga q (móvil ya que la varilla es conductora) situada a
una distancia r del punto de giro lleva una velocidad lineal
tangencial igual a ![]() y puesto que la varilla se mueve dentro
de una campo magnético que es perpendicular a ella, sobre la carga
q actúa una fuerza (de Lorentz) igual a
y puesto que la varilla se mueve dentro
de una campo magnético que es perpendicular a ella, sobre la carga
q actúa una fuerza (de Lorentz) igual a