
Es evidente que las estructuras poliedrales están presentes en la naturaleza. Todos estamos familiarizados con la forma poligonal de las telarañas, con la estructura hexagonal de los paneles de abejas o la estructura poligonal que conforma la superficie de las alas y ojos de algunos insectos. También los granos de polen y las semillas de ciertas plantas tienen formas poliedrales basadas fundamentalmente en pentágonos y hexágonos, y llama la atención la belleza de seres como los radiolarios (cuyo esqueleto contribuye a la formación de sedimentos marinos) proporcionada por sus formas poliedrales, en algunos casos estrelladas, que en muchas ocasiones van encajándose para formar colonias de gran estabilidad.
Quizás no tan explícitamente, pero sí de un modo muy fuerte, donde aparece una conexión con los poliedros es en el campo de la virología, objeto de estudio de numerosos grupos de investigación en la actualidad y en el que vamos a centrarnos a continuación.
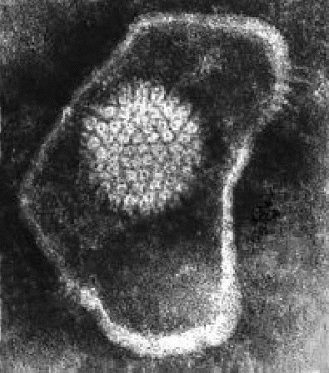
Los virus son microorganismos formados por asociaciones organizadas de macromoléculas, sólo visibles con microscopio electrónico debido a su pequeño tamaño (entre 10 y 300 nanómetros), que se caracterizan por poseer solamente un tipo de ácido nucleico, ADN o ARN, pero no ambos como ocurre en formas superiores de vida. El ácido nucleico que contiene el material genético está protegido por una capa proteica que se llama cápside, la cuál está compuesta de numerosas subunidades proteicas sujetas a ciertas simetrías que determinan que la cápside adquiera una estructura poliedral, que varía de unos virus a otros, lo suficientemente eficaz como para formar un sello capaz de envolver al ácido. Ésta es la composición esencial de todos los virus, aunque algunos más complejos poseen otra envoltura exterior que contiene lípidos y azúcares ligados a las proteínas de la cápside (virus envueltos). La Figura 8 muestra a la izquierda la imagen de un virus envuelto (herpesvirus), en la que puede apreciarse difusamente la forma poliedral de la cápside que vemos con mayor detalle en la imagen de la derecha.


Por sí mismo, un virus (o más precisamente una partícula viral completa: cápside conteniendo al ácido -virion-) puede considerarse como un complejo bioquímico inerte. Depende enteramente de factores externos para poder moverse y no puede replicarse fuera de una célula viva. Cuando ha invadido una célula, el ácido nucleico del virus, que porta la información genética (genoma), dirige la maquinaria de la célula para sintetizar completamente nuevas partículas virales idénticas a la progenitora.
El estudio de los virus como ciencia es relativamente joven, con avances muy rápidos a partir de los años cincuenta en paralelo con los de la biogenética y biología molecular. Hoy en día la clasificación de los virus se hace atendiendo esencialmente a estos dos aspectos: la naturaleza de su material genético y la simetría y composición de su cápside.
Las complejas uniones de macromoléculas en el sello de un virus son maravillosas miniaturas de arquitectura molecular y los requerimientos específicos de cada virus dan como resultado una fascinante diversidad de organización y diseño geométrico en la estructura poliedral asociada. La teoría sobre la construcción de la estructura poliedral de los virus fue iniciada en 1956 por Crick y Watson y estaba basada en algunas consideraciones teóricas y un número no muy grande de evidencias experimentales posibles en aquella época; posteriormente su teoría, en términos generales, sería ampliamente confirmada y universalmente aceptada. Esencialmente, consistía en señalar que la cápside del virus adquiere una estructura poliedral que está determinada por el propio virus y que la forma más económica y ``razonable'' de que el genoma codifique la construcción de la cápside es que para ello utilice el mismo tipo de moléculas una y otra vez (teoría de las subunidades idénticas). Además, estas subunidades deberían empaquetarse siguiendo unas reglas de simetría geométrica de manera que conformaran un sello estable.
En principio pensaron que siempre se empaquetaban siguiendo una simetría icosaedral 5:3:2 (recordemos que el icosaedro está compuesto por veinte triángulos equiláteros y tiene seis ejes de simetría rotacional de 5 hojas que pasan por los vértices, diez ejes de 3 hojas en el centro de los triángulos y quince ejes de 2 hojas en el centro de las aristas) y señalaron que el número de subunidades debería ser un múltiplo de sesenta y que ninguna debería coincidir con un eje.
Con la introducción de las técnicas de coloreado en el microscopio electrónico (Brenner y Horne, 1959) se descubrió la forma de muchas partículas virales y se acordaron los nombres de ``cápside'', ``capsómero'' y ``virion'' (propuestos por Lwoff, Anderson y Jacob, 1959) para denominar respectivamente al sello proteico, a las unidades morfológicas comprendidas en él y a la partícula viral completa. Casi todas las partículas virales analizadas presentaban simetría icosaedral, pero el número de las unidades morfológicas (abultamientos que presenta la cápside) no era en general un múltiplo de sesenta y además estaban localizadas en los ejes de simetría. La aparente paradoja estructural que se presentó, (los capsómeros no eran las subunidades estructurales de las que hablaban Crick y Watson), desapareció posteriormente y se fundamentó en trabajos de Horne y Wildy (1961) y de Caspar y Klug (1962), que en términos generales ratificaban la primitiva teoría de Crick y Watson, a partir de los cuales se unificó la terminología y el análisis de la estructura poliedral de los virus. Así, las ``unidades de estructura'' son las más pequeñas unidades de construcción de la cápside funcionalmente equivalentes y los ``capsómeros'' son las unidades morfológicas que pueden apreciarse en la superficie de la partícula viral y están formadas por distintas agrupaciones de unidades de estructura. El hecho de que las subunidades proteicas no se distribuyan aleatoriamente sino que se adhieran formando capsómeros es debido a que se maximizan las interacciones moleculares que estabilizan la partícula. La unión entre las subunidades adheridas en cada capsómero es más fuerte que la que se da entre unos capsómeros y otros (esto hace que puedan aislarse más fácilmente los capsómeros para posibles estudios funcionales o estructurales).
Aunque algunos presentan una estructura algo más compleja, la mayor parte de los virus corresponden a dos grupos morfológicos diferenciados: Los de simetría helicoidal y los de simetría icosaedral.
En los que presentan simetría helicoidal se observa que tienen una forma tubular hueca y en el hueco es donde se sitúa el ácido. Pero la disposición de las subunidades proteicas en la pared tubular (a excepción de los extremos) no es cilíndrica sino que van conformando una hélice (espiral) que puede ser levógira o dextrógira, cuyos radios circulares y número de unidades por giro de la hélice varía de unos virus a otros.
Los virus con simetría icosaedral (por lo que se conoce hasta la fecha, la preferida por la mayoría) tienen forma esférica y presentan siempre 60T subunidades de estructura formando la cápside. Se dice que T es el número de la triangulación, y toma valores de la serie 1,3,4,7,9,12,13,..., obtenida a partir de la fórmula T = Pf2, donde f es cualquier entero positivo y P cualquier número de la serie 1,3,7,13,19,21,... ( = h2 + hk + k2 , para enteros positivos h y k coprimos). La morfología de la cápside pueden presentarse como 60T monómeros o presentarse como 30T dímeros, 20T trímeros o conformando 10(T-1) hexámeros y exactamente 12 pentámeros.
Actualmente existen técnicas de simulación que permiten reconstruir en un ordenador la forma de muchos virus. Estas imágenes virtuales facilitan el estudio geométrico de su estructura y con ello el análisis de diferentes propiedades del virus investigado. En algunas de las direcciones electrónicas que incluimos al final del trabajo existe una buena colección de imágenes de virus donde pueden observarse diferentes estructuras poliedrales, todas ellas de una enorme belleza. En la Figura 9 aparecen imágenes de dos partículas que corresponden a unas de las primeras enfermedades virales estudiadas; a la izquierda la del virus de la fiebre aftosa -Löffler, 1898- (que presenta simetría icosaedral) y a la derecha la del virus del mosaico del tabaco -A. Mayer, 1886- (que presenta simetría helicoidal). Como curiosidad, incluimos en la Figura 10 la imagen de un virus icosaedral T = 1 (satellite tobacco necrosis virus) cuya forma es similar a la de una de las piedras talladas del neolítico de las que se presentaba una imagen en la sección 2.


Para evaluar la importancia que tiene la determinación de la estructura poliedral de los virus hay que tener en cuenta que éstos, debido a su proceso de reproducción, están obligados a ser parásitos intracelulares; necesitan una célula hospedadora donde replicar su ácido nucleico y tomar la maquinaria sintética para reproducirse completamente y transmitirse a otras células. En este proceso, donde el metabolismo del organismo afectado se perturba, la cápside o poliedro proteico del virus protege a éste del exterior, pero a la vez es una parte fundamental que el organismo invadido reconoce para crear anticuerpos. Además, la morfología de la cápside con protuberancias y hendiduras, que se corresponden con la estructura poliedral, determina las zonas de mayor o menor accesibilidad para los anticuerpos que el sistema inmunológico del receptor puede crear.
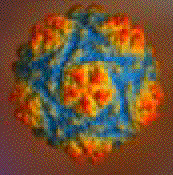
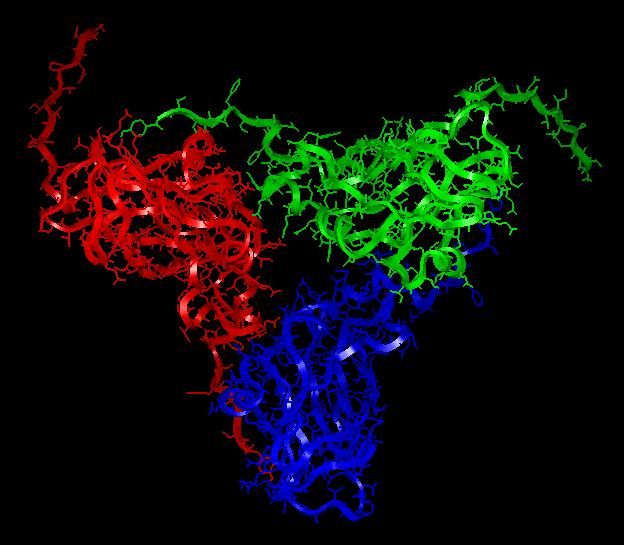
En la Figura 10 aparece a la derecha la imagen de un virus denominado con las siglas CCMV (Cowpea Chlorotic Mottle Virus) al que corresponden las imágenes que mostraremos a continuación. Lo hemos elegido porque su estructura poliedral es exactamente un icosaedro truncado y puede apreciarse bien en la mencionada figura, que muestra la forma global de la partícula viral. Comentaremos muy esquemáticamente cómo se genera la estructura de este virus concreto como ejemplo que puede ilustrar lo que ocurre en general. La cápside del CCVM consta de 180 subunidades proteicas que tienen una composición química idéntica pero la proteína que las forma no adopta la misma conformación geométrica. Se distinguen de tres tipos: A, B y C. Precisamente la diferente conformación de estos tipos de subunidades determina la manera en la que se van a enlazar unas con otras para formar el sello protector del ácido. Matemáticamente, la unidad generadora de la estructura poliedral sería el trímero ABC, que se esquematiza como un triángulo dividido en tres regiones equivalentes A, B y C, coloreadas en gris oscuro o azul, gris o rojo y gris claro o verde respectivamente. Véase la Figura 11.
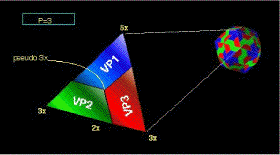
A partir de esta unidad geométrica triangular puede obtenerse la estructura poliedral más básica del virus, que presenta simetría icosaedral, como se observa en la Figura 12. Ahora bien, si tenemos en cuenta la disposición de las diferentes subunidades A, B, C en esta triangulación básica, podemos notar que se forman doce pentámeros, cada uno con cinco subunidades A, y veinte hexámeros, cada uno con tres subunidades B alternándose con tres subunidades C. Véanse las Figuras 12, 13.
>
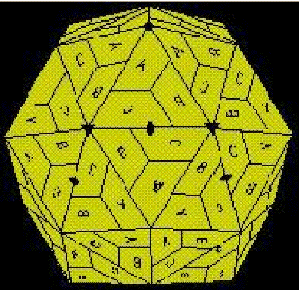
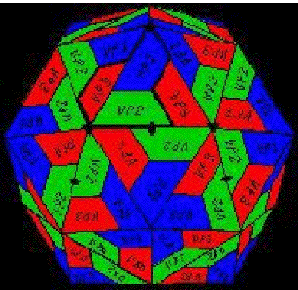

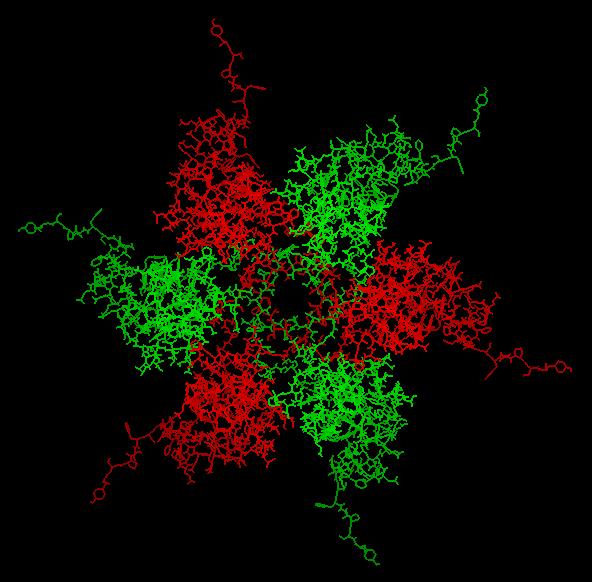
Aparece de este modo una estructura poliedral más fina, en el sentido de que describe más exactamente la conformación final de la cápside viral a partir de las subunidades elementales. En la Figura 14 se ve a la izquierda el esquema del poliedro final (icosaedro truncado) y a la derecha la silueta de éste sobre la imagen del virus.

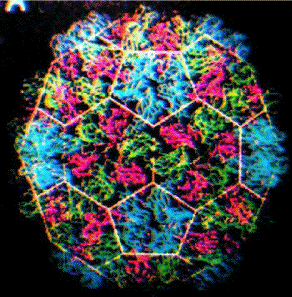
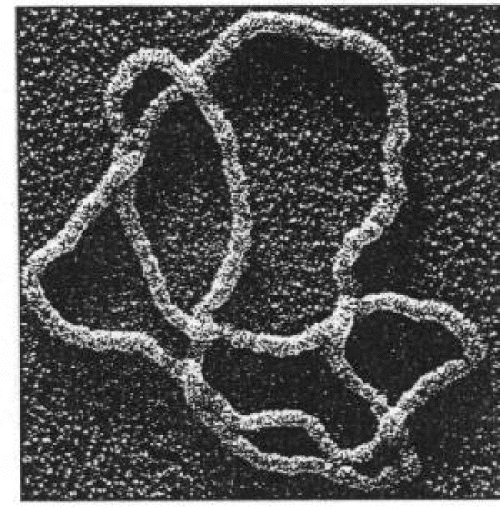
Muchos de los trabajos sobre virus que hemos analizado contienen, cuando es posible, la representación de la unidad geométrica estructural y el tipo de simetría que experimenta para formar el sello (mapa topográfico); esto determina la disposición de las subunidades proteicas y con ello la forma poliedral final del virus. Por otra parte, el ácido envuelto por la cápside de los virus, que se presenta como una madeja filamentosa de una o más hebras, es susceptible de ser estudiado con técnicas topológico-geométricas, fundamentalmente teoría de nudos. Véase la Figura 15. Existen actualmente trabajos en este sentido encaminados al análisis de los anudamientos o enlaces topológicos que presenta un ácido viral (u otro tipo de ácido genético) y sus posibles modificaciones en fenómenos de replicación o en experimentos de manipulación genética. Así, en el estudio matemático de los virus se suelen considerar dos estructuras poliedrales: la externa (poliedro de la cápside) y la interna (grafo del ácido) que pueden ser analizadas geométrica y topológicamente.


La difusión de los virus en la naturaleza es enorme. Si tenemos en cuenta que numerosas enfermedades del hombre (desde el resfriado común y la gripe hasta ciertas meningitis, hepatitis, sida, algunos cánceres, etc) son causados por virus y que lo mismo ocurre con los animales y las plantas, no es extraño que Peter B. Medawar, Premio Nobel de Medicina en 1960, definiera de modo rápido a los virus así: ``Una mala noticia envuelta en proteínas''. Esta definición, avalada a diario en cualquier consulta médica o en los medios de comunicación, recoge el aspecto negativo que en general tienen los virus y motiva el interés por su conocimiento completo con vistas al control y curación de enfermedades causadas por ellos; pero no aborda sin embargo el aspecto positivo que en ciertos ámbitos tienen. Por ejemplo, la gran cantidad de colorido que desde el siglo XVI ofrecieron los tulipanes holandeses se debió a una enfermedad vírica; y, en otro sentido, el hecho de que numerosas enfermedades virales afecten a insectos (un número grande de ellas se recoge precisamente bajo el nombre genérico de ``poliedrosis'') de forma muy selectiva, o, que para algunas actúen como vector de transmisión, está abriendo el campo para su utilización como agentes naturales de control biológico. Es tan amplia la influencia de los virus que justifica que este campo de investigación sea uno de los más interesantes y pujantes en la actualidad y que en él aparezcan estudios relativos a la estructura poliedral asociada a los virus analizados, pieza importante para su conocimiento. Además estos trabajos involucran a disciplinas tan diversas como matemáticas, informática, biología, química, medicina, veterinaria, ecología, ciencias agrícolas y forestales o economía.

En la naturaleza aparecen también estructuras poliedrales (algunas de las cuales son poliedros regulares) como cristales de diversas sustancias. Por ejemplo, el cubo aparece en los cristales de sal común, el tetraedro en los del sodio sulfantimoniato, el octaedro en los del alumbre de cromo, y el dodecaedro (no del todo regular) en los de la pirita. Es por ello que los poliedros se han utilizado siempre en temas cristalográficos relacionados fundamentalmente con la geología y la química.
Hoy en día, además de lo señalado anteriormente en el caso de los virus, muchas investigaciones abordan el estudio de estructuras poliedrales que aparecen en los campos de la biología y química moleculares y de la física nuclear. Las propiedades de estas estructuras poliedrales están relacionadas con las de los materiales analizados. Por ejemplo, la dureza y las propiedades magnéticas, aislantes o conductoras están directamente relacionadas con la estructura poliedral de las moléculas y substancias consideradas. Y en el análisis de las posibles estructuras poliedrales asociadas a los materiales, los invariantes algebraicos y geométricos pueden clarificar algunas propiedades químicas o físicas de éstos.
Empezaremos analizando, en el campo de la química, las estructuras poliedrales más sencillas. Una de las más simples es la de grafo, es decir, un poliedro o complejo celular unidimensional. Su uso es frecuente en el estudio del fenómenos moleculares; por ejemplo, se puede asociar un vértice con cada átomo y una arista con cada enlace (no importando la clase de enlace considerado). Con esta estructura, cada molécula estable determina un grafo conexo. Es fácil comprender la estrecha relación que existe entre la familia de los grafos finitos y conexos, módulo isomorfismo, y las posibles estructuras moleculares. En el caso en el que la estabilidad se alcance con un gran número de átomos, el uso de grafos infinitos puede modelar mejor la estructura poliedral de la substancia analizada.
Sin embargo, es posible asociar a cada molécula o substancia estructuras poliedrales más complejas. Por ejemplo, cada elemento químico determina un subconjunto de vértices; o bien un tipo de enlaces, digamos enlaces covalentes dobles, determina unas aristas que definen un subpoliedro. Por otro lado, a algunos ciclos generados por sucesiones alternadas de átomos y enlaces que finalicen en el átomo inicial de la sucesión, se les pueden asociar caras de dimensión dos. También se pueden asociar caras mediante otros criterios; por ejemplo, considerando átomos de un mismo elemento próximos entre sí que sean coplanarios y que determinen un polígono convexo. Del mismo modo, existen partes de una molécula o de una substancia que tienen una estructura fija, la cual determina un grupo funcional al que a su vez se le puede asociar un subpoliedro.
Una vez establecidos los criterios para asociar una estructura poliedral a una molécula o a una substancia, se tiene que algunas de las propiedades quedan reflejadas en la estructura poliedral asociada y, en general, ésta puede ser más compleja que un solo poliedro y contener subpoliedros asociados con grupos funcionales determinados. En muchas ocasiones la estructura poliedral correspondiente está inmersa en el espacio euclídeo, lo que permite, estudiando sus grupos de simetría, analizar diversas cuestiones como por ejemplo la estructura de los empaquetados de los átomos y moléculas. La disposición ordenada de cationes y aniones está relacionada con las propiedades magnéticas de la substancia considerada. La disposición de los enlaces en varias capas planas o en redes espaciales tiene que ver con la dureza del material considerado.
Otro aspecto interesante es el de la isomería, es decir, aquellos fenómenos asociados con substancias que tienen esencialmente los mismos componentes pero éstos admiten distintas disposiciones geométricas, lo que puede originar diferentes propiedades. Por ejemplo, dos núcleos con igual masa y número atómico pueden presentar distintas propiedades, a causa de una estructuración diferente de sus componentes.
Actualmente existen herramientas que permiten desvelar la estructura poliedral de muchas substancias. Se dispone de diferentes tipos de rayos, aceleradores, microscopios electrónicos, reactores nucleares y otras técnicas de tipo físico o químico.
De modo general señalaremos que en la estructura poliedral intervienen decisivamente el tamaño de los átomos y de los cationes y aniones y el tipo y capacidad de enlace que tengan los elementos que forman la substancia a analizar. Además, a veces es interesante tener en cuenta que el tamaño y tipo de enlaces puede ser modificado por la temperatura, presión u otros factores que afecten al material considerado.
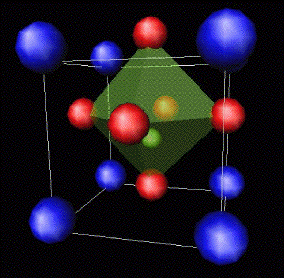
Por ejemplo, el grupo de las perovskitas tiene fórmula general ABX3, donde A y B son cationes y X es un anión (generalmente oxígeno), véase la Figura 16. Los cationes de tipo A ocupan los vértices de una teselación cúbica del 3-espacio euclídeo. Los baricentros de estos cubos están ocupados por cationes de tipo B. Obsérvese que cuando el número N de cationes B es muy elevado, puesto que cada vértice es compartido por ocho cubos, se tiene que el número de cationes de tipo A es N8/8. Considerando que el cubo tiene seis caras y cada cara es compartida por dos cubos, el número de caras será de N6/2. Esta disposición de los vértices y caras de la teselación cúbica es totalmente coherente con la fórmula general de la perovskita N(A8/8BX6/2). Cuando los radios de los cationes y los aniones lo permiten, los aniones X se sitúan en los centros de las caras; de este modo, en cada cubo éstos expanden un octaedro cuyos vértices son de tipo X, de modo que en su interior está contenido un catión B.
Son muy interesantes los siguientes fenómenos determinados por las leyes naturales de los empaquetamientos. Si los cationes de tipo A son de radio grande, no es posible que los planos que contienen cationes de este tipo contengan simultaneamente aniones de tipo X; se producen entonces traslaciones horizontales y verticales que desplazan los aniones de los centros de las caras, generándose planos alternados de cationes y aniones que determinan una polarización magnética de la perovskita analizada. Una substancia magnéticamente estable sometida a un cambio de temperatura puede cambiar sus propiedades magnéticas si se producen estos desplazamientos de los aniones que abandonan los centros de las caras. En cambio, cuando los cationes de tipo A son pequeños, el octaedro interno puede girar un poco, lo que permite alcanzar un equilibrio magnético.

Una reciente rama de la química, especialmente rica en investigación y en la que el uso de técnicas poliedrales es muy amplio, es la de los fullerenos. Este campo se inició con el descubrimiento en 1985 de la molécula C60, que fue bautizada con el nombre de buckminsterfullereno, y abreviadamente se le llama fullereno, en honor del arquitecto R. B. Fuller. Véase la Figura 16. Esta molécula consiste en 60 átomos de carbono unidos mediante doce pentágonos y veinte hexágonos. Su forma es la misma que la de un balón de fútbol y aproximadamente su tamaño es al del balón como el de éste es al de la Tierra; en este caso la estructura poliedral es muy simple, en el sentido de que consta de un solo poliedro que es un icosaedro truncado.
La molécula C60, llamada por muchos ``la más bella molécula'', fue descubierta por los investigadores H. W. Kroto, R. E. Smalley y R. F. Curl en 1985 cuando hacían estudios sobre la composición química de las estrellas. Al analizar las imágenes obtenidas por los telescopios de los observatorios astronómicos, ellos sospechaban, al igual que otros científicos, que tal composición tenía que ver con largas cadenas de moléculas de carbono. En lugar de obtenerlas por simulación mediante experimentos con técnicas convencionales, los investigadores señalados decidieron pasar un haz de láser sobre el vapor de carbono; al hacerlo, no sólo aparecieron las cadenas de moléculas que esperaban, sino que observaron que éstas tenían una forma poliédrica totalmente inesperada, como la de un balón de fútbol. Así se descubrió el C60. Estas moléculas de C60 se condensan en una forma nueva de carbono sólido, una forma cristalina de carbono puro diferente de los conocidos diamante o grafito.
Aunque inicialmente el C60 sólo podía producirse en muy pequeñas cantidades, lo cuál restringía su uso para otros experimentos, W. Krätschen, L. Lamb, K. Fostiropoulos y D. Huffman descubrieron en 1990 el modo de producirlo en mucha mayor cantidad, lo que abrió nuevas posibilidades para las investigaciones experimentales.
El descubrimiento del C60, hecho por el cuál sus descubridores recibieron el Premio Nobel de Química en 1996, ha sido el inicio de un periodo de gran actividad en la química de los llamados fullerenos (compuestos de moléculas de carbono formadas con diferente número de átomos que generan estructuras poliedrales con caras pentagonales, hexagonales o incluso heptagonales). Posteriormente también se han sintetizado otros muchos fullerenos: C70, C76, C78, C82, C84, etc. Muchos trabajos se centran en los fullerenos debido a que al añadirles ciertos átomos alcalinos se obtienen compuestos superconductores eléctricos.
Actualmente hay abierto un nuevo campo de investigación que permite el estudio de los posibles fullerenos a través de herramientas matemáticas tales como la teoría de grafos, poliedros, topología algebraica, teoría de grupos y geometría diferencial; en este sentido, existe una importante relación entre la clase de superficies orientadas y conexas regulares con caras pentagonales, hexagonales y heptagonales, módulo isomorfismos poliedrales, y los posibles compuestos de carbono puro del tipo anterior.
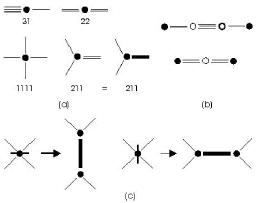
Del carácter tetravalente del carbono C resultan cuatro posibles situaciones de un vértice que denotaremos por 31, 22, 211 y 1111 (Figura 18). Es habitual asociar a cada compuesto puro de carbono un grafo de modo que los carbonos se corresponden con los vértices y los enlaces con las aristas. La situación 31 se puede obtener considerando grafos lineales o en forma de circunferencia en los que se van alternado el enlace triple y el enlace sencillo. El enlace 22 también genera cadenas lineales o circulares en las que alternan átomo y doble enlace. En la mayoría de los fullerenos todos los enlaces son del tipo 211; en consecuencia, sus grafos asociados tienen la propiedad de que cada vértice incide con tres aristas (grafos 3-regulares). No obstante, a cada fullereno se le pueden asociar estructuras poliedrales más complejas; es frecuente añadir una cara por cada grupo de vértices y aristas que determinan un polígono plano convexo. De este modo, cada compuesto del carbono con enlaces de tipo 211 tiene asociada una superficie. Estas superficies se pueden agrupar por capas o a través de empaquetamientos.
En los grafos 3-regulares se pueden distinguir los enlaces dobles coloreando la familia de aristas que se corresponden con los mismos. También es frecuente utilizar la relación que existe entre grafos 3-regulares y grafos 4-regulares. Nótese que si en un grafo 3-regular con aristas coloreadas, se deforma cada arista coloreada a un punto, se obtiene un grafo 4-regular. Recíprocamente, si a un grafo 4-regular le aplicamos un proceso de bifurcación en cada vértice como se señala en la Figura 18 se obtiene un grafo 3-regular con aristas coloreadas.
Es interesante señalar que a cada grafo 3-regular se le puede asociar su grupo de isometrías y, si se tienen aristas coloreadas (enlaces dobles), tomar entonces el subgrupo de aquéllas que las preservan. De este modo a cada grafo con aristas coloreadas le hemos asociado una pareja de grupos. Observemos que si en el mismo grafo 3-regular cambiamos de familia de aristas coloreadas (es decir, consideramos dos isómeros) puede suceder que el subgrupo asociado sea distinto. Sin embargo, existen ejemplos de grafos 3-regulares con aristas coloreadas que son distintos y tienen asociada la misma pareja de grupos de simetría; en este caso, se puede diseñar una herramienta matemática más fina capaz de distinguir estos isómeros. Se procede del modo siguiente: cambiando cada enlace doble por un cruce elevado de caminos, podemos asociar a cada fullereno con enlaces químicos dobles un enlace o nudo topológico susceptible de ser estudiado con técnicas homotópicas. Véase la Figura 19. Las diferentes posibles posiciones de los dobles enlaces químicos determinan enlaces topológicos distintos y la clasificación de estos isómeros se aborda a través de los invariantes homotópicos del enlace o nudo topológico asociado. Utilizando el grupo fundamental del complemento del enlace o sus invariantes de tipo polinómico se pueden distinguir isómeros con grupos de simetría iguales.

En el caso en el que las moléculas estables adquieran forma de superficie, es también importante la disposición que puedan presentar estos enlaces. En algunos casos las caras se unen entre sí para formar superficies con curvatura gaussiana de diferentes signos; en el caso de los grafitos se suelen presentar superficies planas. Se ha observado que por lo general las caras pentagonales corresponden a zonas de curvatura positiva, las hexagonales se relacionan con curvatura cero, y las heptagonales con curvatura negativa.
En la Figura 20 puede verse a la izquierda la superficie de un fullereno contenida en el plano hiperbólico y a la derecha la de un fullereno contenido en un toro en la que se observa claramente cómo las caras pentagonales, hexagonales y heptagonales se distribuyen en zonas con curvatura gaussiana positiva, nula o negativa respectivamente.

Los ejemplos mencionados son una muestra de los cada día más abundantes trabajos de investigación en los que se emplean técnicas matemáticas relacionadas con las estructuras poliedrales asociadas a las moléculas y substancias, tanto para descubrir propiedades de las ya sintetizadas, como para la predicción de otras nuevas.


Si lo expuesto anteriormente muestra de alguna forma cómo los poliedros están muy presentes, aunque de un modo oculto a veces, en las ciencias mencionadas, es evidente su presencia e importancia en otros campos más próximos a la mayoría de las personas. Por ejemplo, en el diseño industrial las propiedades de estructuras poliedrales han de tenerse en cuenta tanto para la fabricación, empaquetado, almacenaje o economía. Quizás aún es más evidente esto en el diseño arquitectónico, desde los edificios y poblados más sencillos hasta las edificaciones y ciudades más sofisticados, y no es una simple anécdota el hecho de que la molécula C60, cuyo descubrimiento ha supuesto un verdadero avance en campos científicos importantes, recibiera el nombre de fullereno precisamente en honor del arquitecto Richard Buckminster Fuller (1895-1983). Véase la Figura 21.
La belleza poliedral del C60 les recordaba a sus descubridores la de las famosas ``cúpulas geodésicas'' diseñadas por Fuller. Siguiendo la pauta de que una esfera es realmente eficiente pues encierra el mayor volumen con la menor superficie y que las geodésicas en una superficie son las curvas de menor longitud entre dos puntos, las edificaciones geodésicas que diseña Fuller adquieren su estructura poliedral a partir de piezas básicas que van encajándose de modo que se obtenga la máxima ventaja estructural y ambiental con un coste reducido. Una muestra de esto es el Pabellón de los Estados Unidos en la Expo 67 de Montreal, que puede verse en la Figura 21. Fuller no sólo ha sido un famoso arquitecto del siglo XX, sino un hombre de espíritu renacentista con obras de ingeniería y diseño en campos tan diversos como el industrial, espacial, automovilístico o cartográfico. Procuró difundir las ideas humanísticas y ecológicas que impregnan su obra a través de múltiples conferencias por todo el mundo, por lo que llegó a ser un personaje controvertido, idolatrado por muchos y denostado por otros, pero con una influencia incuestionable.



Por último vamos a referirnos, aunque sea muy brevemente, a la presencia de los poliedros en el ámbito de las Matemáticas, donde, si bien su estudio se ha hecho inicialmente, como el de la mayoría de los temas antiguos, dentro del campo de la Geometría, estos objetos aparecen hoy en día en diversas áreas, abordando su análisis con las diferentes herramientas que ellas ofrecen o utilizándolos como soporte para la resolución de otros problemas específicos.
Como hemos señalado al inicio de este trabajo, desde muy antiguo han llamado la atención las figuras poligonales o poliedrales que presentaban algún tipo de regularidad y los matemáticos han intentado dar respuesta a diferentes cuestiones tales como la existencia y construcción de estos objetos.
Cualquier polígono regular puede imaginarse como el resultado de dividir una circunferencia en n partes iguales (n ³ 3) y tomar alternativamente los puntos de división obtenidos de p en p, siendo p cualquier primo con n menor que n/2 (se dice que n es el género y p la especie del polígono). En el que caso en el que p = 1 se obtiene un polígono convexo y en otro caso uno estrellado. El número total de polígonos regulares de género n es N/2 donde N es indicador de n. Respecto a la posibilidad de construir con regla y compás los polígonos regulares, Euclides, en sus Elementos, dio la del triángulo equilátero en el Libro I (Prop. 1) y la del cuadrado, pentágono, hexagóno y uno de quince lados en el Libro IV (Prop. 6, 11, 15 y 16 respectivamente); y la Proposición 9 del Libro I garantiza la duplicación sucesiva del número de lados por bisección. El problema abierto de la construcción con regla y compás del resto de polígonos regulares fue parcialmente resuelto por Gauss (quien construyó a los diecinueve años uno de diecisiete lados) afirmando que es condición suficiente que los factores primos impares de n sean primos de Fermat diferentes entre sí (un número de Fermat tiene la forma Fk = 22k +1). En 1837, Wantzel probó que también la anterior condición es necesaria.
En el caso de los poliedros el grado de regularidad viene dado por la forma, número y disposición de caras y vértices. Se dice que dos vértices de un poliedro son idénticos si ambos están rodeados por el mismo número y tipo de caras y en el mismo orden. Si todos los vértices son idénticos y además todas las caras son polígonos regulares iguales se dice que el poliedro es regular. Desde muy antiguo se conocía que existen solamente cinco poliedros regulares convexos, los famosos Sólidos Platónicos. Respecto a la existencia de poliedros regulares no convexos, Kepler [20] describió dos: el pequeño y el gran dodecaedro estrellados; y Louis Poinsot en 1809 redescubrió los anteriores y descubrió otros dos: el gran dodecaedro y el gran icosaedro. Cauchy, en 1813, demostró que los cuatro anteriores son todos los posibles poliedros regulares estrellados.
Rebajando la exigencia de regularidad, dentro de los poliedros convexos, reciben el nombre de Sólidos Arquimedianos o Semiregulares aquellos cuyos vértices son idénticos y las caras son polígonos regulares de dos o más tipos diferentes, excluyendo las familias infinitas de los prismas y los antiprismas. Kepler se ocupó especialmente de este tipo de poliedros, entre los que se encuentra el notable icosaedro truncado. En 1619 dio la lista, demostrando que era completa, de los 13 sólidos de este tipo que existen, aunque 12 de ellos ya habían sido redescubierto por distintos artistas del Renacimiento. Se les llama Arquimedianos porque se sabe que fueron estudiados por Arquímedes, aunque sus trabajos originales están perdidos. Se llama dual de un poliedro dado a un nuevo poliedro en el que las caras y vértices corresponden respectivamente a vértices y caras del original. Los poliedros duales de los Arquimedianos se llaman Sólidos de Catalan [2], que fue quien los descubrió en 1865; obviamente hay 13 y sus caras no son polígonos regulares.
Continuando con la idea de caras regulares y vértices idénticos, pero admitiendo la posibilidad de caras que sean polígonos no convexos, se obtienen los Poliedros Uniformes. En 1954 Coxeter [7] conjeturó, y fue posteriormente probado por Skilling [24], que hay 75 (sin contar prismas ni antiprismas).
Si nos restringimos a poliedros convexos y nos preguntamos cuántos hay que tengan las caras regulares, además de los Sólidos Platónicos, los Arquimedianos, y las familias infinitas de prismas y antiprismas, la respuesta es que hay 92 más, los cuales reciben el nombre de Sólidos de Johnson [18], quien en 1966 dio la lista y además conjeturó que era completa, lo que fue probado en 1969 por Zalgaller [28].
Los ejemplos anteriores determinan diferentes triangulaciones en una esfera topológica. En la sección 2 aparecía la figura de una superficie tórica descompuesta en polígonos; del mismo modo, numerosos espacios (algunas variedades, variedades con singularidades, etc.) admiten descomposiciones (triangulaciones) en piezas más sencillas de dimensiones adecuadas. La generalización de estas ideas da lugar a diversas nociones geométricas, topológicas y algebraicas, que genéricamente pueden denominarse ``estructuras poliedrales'' o ``poliedros'', como son los complejos simpliciales, complejos de celdas, conjuntos simpliciales, etc.
Dentro del área de la Topología Algebraica, en la que concretamente se enmarca nuestra actividad, las estructuras poliedrales juegan un importante papel. Desde las más rígidamente geométricas, han sido la fuente de inspiración para la creación de teorías de homotopía y homología que después han sido diversificadas, generalizadas o sintetizadas con el objetivo de obtener mecanismos para poder estudiar espacios susceptibles o no de admitir estructuras poliedrales generales más o menos rígidas, como hemos visto que ocurre por ejemplo con el caso de los fullerenos mencionados anteriormente.
Señalemos que si esta estructura poliedral sólo contiene un número finito de piezas básicas, el espacio descrito por ella es compacto; así que si se desea estudiar espacios no compactos, en los que uno puede imaginar escapes hacia el infinito de una o muchas maneras, entonces las estructuras poliedrales llamadas clásicas deben estar hechas de infinitas piezas, lo cuál puede ser un obstáculo a la hora de aplicar técnicas computacionales. Dentro de este último marco, estudio de los espacios no compactos, concretamente en el de la Teoría de Homotopía Propia (del que una visión panorámica puede encontrarse en [17]), se halla parte de nuestra labor de investigación, y en particular algunos trabajos donde proponemos nuevas estructuras poliedrales que incluyen piezas básicas diferentes a las habituales con el fin de obtener posibles descripciones de espacios no compactos con un número finito de piezas.
Por otra parte, también han tenido un fuerte desarrollo los trabajos de programación encaminados a la representación de espacios y al cálculo de invariantes topológicos asociados a estructuras poliedrales que los describen o aproximan. Es un hecho cada vez más frecuente trabajar con técnicas de simulación sobre diferentes fenómenos físicos celulares o moleculares, donde se utilizan formas geométricas iniciales muy sencillas que van adquiriendo mayor complejidad estructural a medida que se avanza en la aproximación al fenómeno real simulado.
Nos gustaría que lo expuesto anteriormente, aunque sólo sea una pequeña muestra, pueda servir para ilustrar hasta qué punto los poliedros están próximos a nosotros y siguen siendo unos objetos matemáticos fascinantes sobre los que merece la pena seguir avanzando en su estudio y utilización.
Terminamos recordando las palabras de Galileo Galilei:
``... La filosofía (naturaleza) está escrita en ese gran libro que siempre está ante nuestros ojos -el universo- pero no lo podemos entender si no aprendemos primero el lenguaje y comprendemos los símbolos en los que está escrito. El libro está escrito en lenguaje matemático y sus símbolos son triángulos, círculos y otras figuras geométricas, sin cuya ayuda es imposible comprender una sola palabra; sin ello uno vaga sin esperanza en un oscuro laberinto ...''