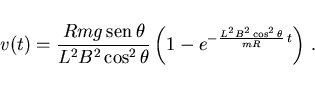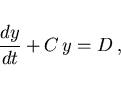 |
(17) |
Ampliación.
Sea la ecuación diferencial
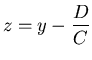 , y puesto que D/C es contante, entonces se
cumple que
, y puesto que D/C es contante, entonces se
cumple que
 .
Con este cambio de variable, la ecuación diferencial queda
.
Con este cambio de variable, la ecuación diferencial queda
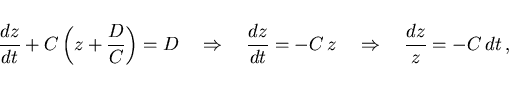

Para los problemas en los que vamos a encontrar esta ecuación
diferencial, y(t) va a ser la velocidad y por tanto la
ecuación diferencial (17) tiene el siguiente sentido
físico: la derivada
![]() es la aceleración
(igual a la fuerza total dividida por la masa), que de acuerdo
con la ecuación diferencial, es igual a una constante menos un
término proporcional a la velocidad.
O sea, la fuerza total que está actuando sobre el cuerpo cuyo movimiento
describe (17) es igual a un término constante (por ejemplo
el peso) más otra fuerza que es proporcional a menos la velocidad,
fuerza ésta que suele describir un rozamiento o amortiguamiento.
De acuerdo con (18), la velocidad inicial del cuerpo es
es la aceleración
(igual a la fuerza total dividida por la masa), que de acuerdo
con la ecuación diferencial, es igual a una constante menos un
término proporcional a la velocidad.
O sea, la fuerza total que está actuando sobre el cuerpo cuyo movimiento
describe (17) es igual a un término constante (por ejemplo
el peso) más otra fuerza que es proporcional a menos la velocidad,
fuerza ésta que suele describir un rozamiento o amortiguamiento.
De acuerdo con (18), la velocidad inicial del cuerpo es
 mientras que la velocidad límite que alcanzará
para
mientras que la velocidad límite que alcanzará
para ![]() es igual a D/C.
Esta velocidad límite se obtiene de manera más directa a partir
de la ecuación diferencial inicial: una vez el cuerpo alcance la
condición límite,
es igual a D/C.
Esta velocidad límite se obtiene de manera más directa a partir
de la ecuación diferencial inicial: una vez el cuerpo alcance la
condición límite,
![]() , su velocidad es
constante y no varía, por lo que la derivada
, su velocidad es
constante y no varía, por lo que la derivada
![]() es cero y a partir de (17) se obtiene
es cero y a partir de (17) se obtiene

Puesto que en la mayor parte de los casos la velocidad inicial es
cero,
y(t=0)=0, la solución general de la ecuación
diferencial que estamos estudiando es

P.48
Inicialmente por la espira cerrada que queda a la derecha circula una
corriente
 donde R es la resistencia de la barra vertical (los dos
conductores horizontales paralelos no tienen prácticamente
resistencia), siendo la dirección de esta corriente hacia abajo en
la barra vertical.
Al moverse esta barra vertical, el flujo que atraviesa la espira
varía con el tiempo y por tanto, a parte de la intensidad inicial,
se inducirá otra intensidad más debida a la Ley de Faraday.
En un intervalo infinitesimal de tiempo dt el
área atravesada por el campo magnético disminuye en vdtL:
por tanto lo que varía el flujo magnético que atraviesa
la espira es
donde R es la resistencia de la barra vertical (los dos
conductores horizontales paralelos no tienen prácticamente
resistencia), siendo la dirección de esta corriente hacia abajo en
la barra vertical.
Al moverse esta barra vertical, el flujo que atraviesa la espira
varía con el tiempo y por tanto, a parte de la intensidad inicial,
se inducirá otra intensidad más debida a la Ley de Faraday.
En un intervalo infinitesimal de tiempo dt el
área atravesada por el campo magnético disminuye en vdtL:
por tanto lo que varía el flujo magnético que atraviesa
la espira es
![]() ,
donde el primer signo menos en
,
donde el primer signo menos en ![]() viene de que el vector de
superficie de la espira va hacia fuera de la hoja (aplicando la regla
de la mano derecha cuando se recorre la espira en la dirección en la
que circula inicialmente la corriente) mientras que el vector campo
mágnetico va hacia dentro.
Por lo tanto, la corriente total que circula por la espira es igual a
la suma de la corriente inicial más la corriente inducida
viene de que el vector de
superficie de la espira va hacia fuera de la hoja (aplicando la regla
de la mano derecha cuando se recorre la espira en la dirección en la
que circula inicialmente la corriente) mientras que el vector campo
mágnetico va hacia dentro.
Por lo tanto, la corriente total que circula por la espira es igual a
la suma de la corriente inicial más la corriente inducida
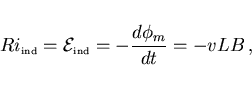

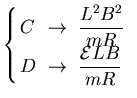 .
Puesto que la velocidad inicial de la barra es cero, la velocidad en
cualquier instante de tiempo viene dada por la solución
(19)
.
Puesto que la velocidad inicial de la barra es cero, la velocidad en
cualquier instante de tiempo viene dada por la solución
(19)
P.51
Como en el problema anterior,
al moverse hacia abajo la barra conductora sobre los raíles
(raíles que se suponen están conectados entre sí en la parte
de abajo), disminuye el número de líneas del campo magnético que
atraviesa la superficie de la espira formada por la barra móvil
y los raíles según


Viendo los raíles paralelos de perfil (que forman un ángulo
![]() con la horizontal), tenemos que sobre la
sección de la barra conductora móvil actúan las siguientes
fuerzas:
con la horizontal), tenemos que sobre la
sección de la barra conductora móvil actúan las siguientes
fuerzas: