

P.1
La carga situada en y=a crea un campo en (x, y=0) igual a

 ; notar que el vector
; notar que el vector
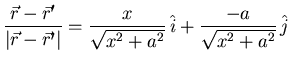 .
La componente vertical del campo eléctrico anterior es compensada por la
componente vertical del campo creado por la carga situada en y=-a
(para verlo, basta con sustituir en la ecuación anterior a por
-a).
El campo eléctrico resultante es entonces
.
La componente vertical del campo eléctrico anterior es compensada por la
componente vertical del campo creado por la carga situada en y=-a
(para verlo, basta con sustituir en la ecuación anterior a por
-a).
El campo eléctrico resultante es entonces
 .
Para
.
Para
P.2
Por el mismo motivo que en el
problema anterior, la dos
cargas Q colocadas en la vertical del punto donde queremos calcular
el campo (donde está situada la carga q) compensan entre sí el
campo eléctrico que crean en el centro del círculo.
La dos cargas siguientes crean un campo que viene dado por la
ecuación (1) para
 ; y la carga
que está sobre el eje horizontal crea un campo también dado por
(1) con x=R y a=0.
El campo resultante en el centro del círculo es entonces
; y la carga
que está sobre el eje horizontal crea un campo también dado por
(1) con x=R y a=0.
El campo resultante en el centro del círculo es entonces
P.3
Midamos el ángulo ![]() a partir del eje vertical.
Un elemento diferencial de arco situado a un ángulo
a partir del eje vertical.
Un elemento diferencial de arco situado a un ángulo ![]() de la
vertical crea un campo en el origen de coordenadas
de la
vertical crea un campo en el origen de coordenadas
 .
.
P.4
Un elemento diferencial dx situado a una distancia x del origen de
coordenadas crea en este último punto un campo
 ya que la carga que tiene dicho elemento
diferencial es
ya que la carga que tiene dicho elemento
diferencial es ![]() .
El campo resultante de sumar toda la distribución continua de carga
es
.
El campo resultante de sumar toda la distribución continua de carga
es
P.5
En el vértice inferior izquierdo el campo creado por cada una de las
cargas (sin contar la carga que está situada en dicho punto) es
Para el segundo caso, el campo eléctrico creado por las cuatro
cargas es
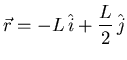 y por tanto el vector
unitario en tal dirección es
y por tanto el vector
unitario en tal dirección es
 .
.
P.6
El campo eléctrico
![]() con
con
![]() indica que la placa superior del condensador plano está cargada
negativamente y por tanto va a repeler al electrón.
Dentro del condensador la fuerza que actúa sobre el electrón es
indica que la placa superior del condensador plano está cargada
negativamente y por tanto va a repeler al electrón.
Dentro del condensador la fuerza que actúa sobre el electrón es
![]() , donde
, donde
![]() es la
carga del electrón, y por tanto estará sometido a una
aceleración
es la
carga del electrón, y por tanto estará sometido a una
aceleración


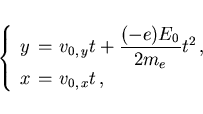
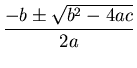 , el que exista solución
depende de si lo que hay dentro de la integral es mayor que cero, ya
que la raíz cuadrada de un número negativo es un número
imaginario.
En nuestro caso, es necesario que
, el que exista solución
depende de si lo que hay dentro de la integral es mayor que cero, ya
que la raíz cuadrada de un número negativo es un número
imaginario.
En nuestro caso, es necesario que
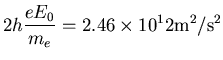 ,
no llega a la placa superior.
,
no llega a la placa superior.
*Suplemento.
Otra manera de obtener el mismo resultado es partiendo de que si el
electrón no parte con energía cinética suficiente, no
llegará a alcanzar la placa superior: de acuerdo con la
conservación de la energía mecánica, lo que varía la
energía cinética del electrón es igual a menos lo que
varía la energía potencial

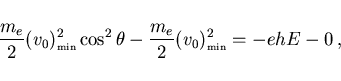
El electrón no alcanza la placa superior y choca contra la placa de
la que partió a una distancia x que viene dada por la ecuación
(9) para y=0: x=0.04 m.
P.7
El campo creado por un elemento diferencial
![]() de carga en un
punto a una altura x del eje viene dado
de carga en un
punto a una altura x del eje viene dado
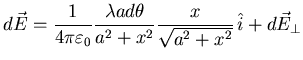 , donde
, donde ![]() es
la densidad lineal de carga
es
la densidad lineal de carga
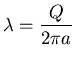 ;
;
![]() es la componente del campo eléctrico perpendicular
al eje X y que al sumar todos los elementos diferenciales de arco se
van a compensar unos con otros, quedando así
es la componente del campo eléctrico perpendicular
al eje X y que al sumar todos los elementos diferenciales de arco se
van a compensar unos con otros, quedando así
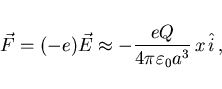
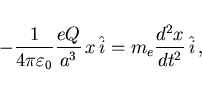
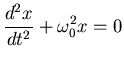 con frecuencia natural
con frecuencia natural
 ; la
frecuencia f viene definida por
; la
frecuencia f viene definida por
P.8
La fuerza de repulsión entre las dos cargas,
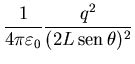 ,
lleva dirección horizontal y en la posición de equilibrio tiene
que ser compensada por la componente horizontal de la tensión,
,
lleva dirección horizontal y en la posición de equilibrio tiene
que ser compensada por la componente horizontal de la tensión,
![]() .
Por otro lado, la componente vertical de la tensión,
.
Por otro lado, la componente vertical de la tensión, ![]() ,
equilibra el peso de cada bola, y por lo tanto
,
equilibra el peso de cada bola, y por lo tanto
P.9
Teniendo en cuenta que la tensión viene dada por
![]() , el peso
por
, el peso
por
![]() , y la fuerza debida al campo
eléctrico constante
, y la fuerza debida al campo
eléctrico constante

P.12
El campo eléctrico creado por el anillo en puntos a lo largo del eje
que pasa por su centro ya ha sido calculado en (12):
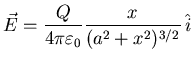 , con Q la carga del anillo.
, con Q la carga del anillo.
 , representada en
trazo continuo en la siguiente figura, presenta un extremo (máximo o
mínimo) en aquellos valores de x para los que la derivada
(representada en trazo discontinuo)
, representada en
trazo continuo en la siguiente figura, presenta un extremo (máximo o
mínimo) en aquellos valores de x para los que la derivada
(representada en trazo discontinuo)
 sea cero, es decir, cuando
sea cero, es decir, cuando