Algebraic aspects of radical parametrizations
J. Rafael Sendra, David Sevilla and Carlos Villarino
$A_1,A_3\in$ SYNACS group (UAH), $A_2\in$ GADAC group (UEx)
Partially supported by the Spanish Ministerio de Economía y Competitividad and by the European Regional Development Fund (ERDF) under project MTM2014-54141-P as well as Junta de Extremadura and FEDER funds (group FQM024).


Radical objects arise naturally in CAGD by performing some operations on rational objects.
Example: offsets


Our goal is to find ways to manipulate algebraic, non-rational (radical) varieties in rational ways.
In this talk we will present our current ideas on
turning radicals into rationals.
The root of the problem
\[\mP(t) = (t,\sqrt{t})\]
Is this the parabola $x=y^2$?
Is $(1,-1)$ a solution of $x=y^2$? in $\Ima(\mP)$?
Behind is our interpretation of the symbol $\sqrt{t}$:
- $\sqrt{1} = 1$
- $\sqrt{1} = -1$ (!)
- $\sqrt{1} = \pm1$
- $\sqrt{1} = \{1,-1\}$
Is the denominator zero in $\left(\displaystyle\frac{1}{\sqrt[6]{t}\sqrt[3]{t}-\sqrt{t}},\,t\right)$ ?
- Yes
- No, except for $t=0$
- Depends on what the $\sqrt[n]{t}$ mean to you
- I feel dizzy already
In the parabola example, $\mP(t) = (t,\sqrt{t})$:
- If $\sqrt{t}$ is either branch (a univalued function) then $\mP$ covers half of $x=y^2$.
- If $\sqrt{t}$ is both branches (a multivalued function) then $\mP$ covers all of $x=y^2$.
Both are reasonable paths.
And so we had to make up our minds...


Definition of radical parametrization
A radical parametrization is a tuple $(x_1,\ldots,x_r)$
of elements of a radical field extension of $\C(t_1,\ldots,t_n)$.
More explicitly...
\[\C(\ot) = \F_0 \subset \F_1 \subset \cdots \subset \F_m\]
where $\F_i = \F_{i-1}(\delta_i)$ with $\delta_i^{e_i}=\alpha_i\in\F_{i-1}$
and $\F_m\ni$ $x_1,\ldots,x_r$$x_1$$(\ot)$$,\ldots,x_r$$(\ot)$
We call the $x_i$ functions because
we think of the $\ot$ as variables.
We also ask that their Jacobian has rank $n$.
Parabola example
$\mP(t) = (t,\sqrt{t})$  Not well defined!
Not well defined!
- Define the tower: $\C(t)\subset\C(t)(\delta_1)$ where $\delta_1^2=t$
- There are two possible $\delta_1$! Fix one by value, say \[\delta_1(+1)=+1\]
- Now $\mP(t) = (t,\delta_1)$ or $\mP(t) = (t,-\delta_1)$

\[(x(t),y(t)) = \left( t+\frac{1-\sqrt[4]{t^3+2t}}{\sqrt{t^2-\sqrt[3]{t-1}}} , \frac{\sqrt[4]{5\sqrt[3]{t-1}+1}}{t^3+5} \right)\]
\[(x(t),y(t)) = \left(t+\frac{1-\delta_4}{\delta_2},\frac{\delta_3}{t^3+5}\right)\]
- $\delta_1^3=t-1$, $\quad\delta_1(2)=1$
- $\delta_2^2=t^2-\delta_1$, $\quad\delta_2(2)=-\sqrt{3}$
- $\delta_3^4=5\delta_1+1$, $\quad\delta_3(2)=i\sqrt[4]{6}$
- $\delta_4^4=t^3+2t$, $\quad\delta_4(2)=\sqrt[4]{12}$
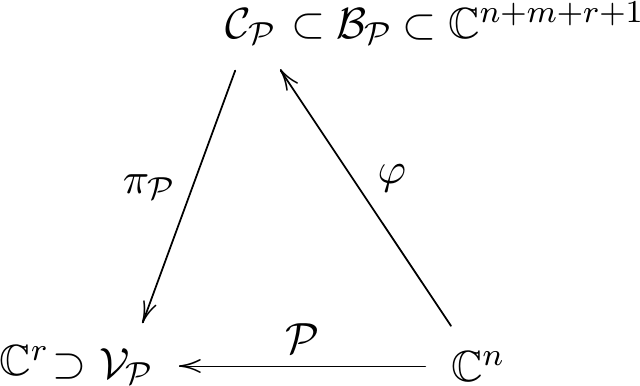
Incidence varieties
Idea: turn those $\delta$'s into variables that
we will relate to the $t$'s.
Incidence varieties
Given a radical parametrization $\mP$, express it as
\[x_i(\ot)=\frac{x_{iN}(\ot,\delta_1,\ldots,\delta_m)}{x_{iD}(\ot,\delta_1,\ldots,\delta_m)} \,,\quad \delta_i^{e_i}=\alpha_i\]
\[\alpha_1=\frac{\alpha_{1N}(\ot)}{\alpha_{1D}(\ot)}, \ \ldots, \ \alpha_m=\frac{\alpha_{mN}(\ot,\delta_1,\ldots,\delta_{m-1})}{\alpha_{mD}(\ot,\delta_1,\ldots,\delta_{m-1})}\]
We define the incidence variety $\BP$ associated to this representation as the zeroset of the polynomials
- $(\Delta_1)^{e_1}\cdot\alpha_{1D}(\OT) - \alpha_{1N}(\OT)$,
$(\Delta_i)^{e_i}\cdot\alpha_{iD}(\OT,\Delta_1,\ldots,\Delta_{i-1})-\alpha_{iN}(\OT,\Delta_1,\ldots,\Delta_{i-1})$ - $X_j\cdot x_{jD}(\OT,\Delta_1,\ldots,\Delta_m) - x_{jN}(\OT,\Delta_1,\ldots,\Delta_m)$
- $Z\cdot \mathrm{lcm}(x_{1D},\ldots,x_{rD}) \cdot \mathrm{lcm}(\alpha_{1D}, \cdots, \alpha_{mD}) - 1$
in the ring $\C[\OT,\Delta_1,\ldots,\Delta_m,X_1,\ldots,X_r,Z]$
Example
\[ \mP = \left(t,\sqrt{1-t^2}\right) \]
\[ \delta^2 = 1-t^2, \ x = t, \ y=\delta \]
\[ \BP = V(\Delta^2-1+T^2, X-T, Y-\Delta, Z-1) \]
We can eliminate everything except $X$ and $Y$:
\[ Y^2+X^2=1 \]
Irreducible component
$\BP$ does not discriminate branches of the $\delta_i$; all possibilities are included.
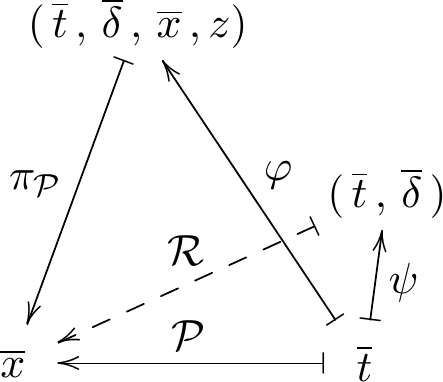
$\BP$ can be reducible (example later). We define $\CP$ as the closure of the image of our branch:
\[ \varphi\colon (\ot) \mapsto (\ot, \bar{\delta}, \bar{x}, z) \]
$\CP = \overline{\Ima(\varphi)} \subset \BP$ and it is irreducible.
Radical variety
The image of a radical parametrization is, intuitively, the evaluation of the $t$'s, the $\delta$'s, and the coordinates as functions of them.
Algebraically, the radical variety defined by $\mP$ is
\[ \VP = \overline{\pi_\mP(\CP)} \]
where $\pi_\mP(\OT,\overline\Delta,\overline{X},Z)=(\overline{X})$
 defined as
defined as 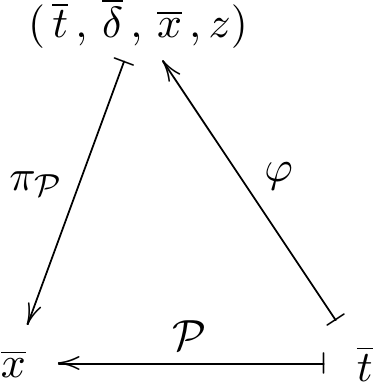
$\VP$ coincides with $\overline{\Ima(\mP)}$, so it does not depend on the representation of $\mP$.
Tricky example
$\mP=(\sqrt[4]{t^2},t)$ where $\sqrt[4]1=1$ (!)
Take the tower $\C(t)\subset \C(\sqrt[4]{t^2})$ (degree 2 extension)
$\BP=V(\Delta^4-T^2,X-\Delta,Y-T,Z-1)$
$V(X^4-Y^2) = V(X^2-Y) \cup V(X^2+Y)$
$\Ima(\mP)$ is half of $V(X^2-Y)=\VP$
The "conjugate parametrizations" $(i^k\sqrt[4]{t^2},t)$, $k=1,2,3$, cover the other three half-parabolas.
Maybe you think that we should not allow
roots that are not simplified...
$\sqrt[4]{t^2} \quad \rightsquigarrow \quad \Delta^4-T^2$ 
$\sqrt{t} \quad \rightsquigarrow \quad \Delta^2-T$ 
So do we, sometimes... 
Can you simplify?
Some properties
- Every component of $\BP$ has dimension $n$, and the number of components is $\leq\prod e_i$ ($\delta_i^{e_i}=\alpha_i$)
- $\Ima(\varphi)$ is contained in only one component of $\BP$, thus $\CP$ is irreducible.
- $\VP$ is irreducible and has dimension $n$.
Tracing index
Looking at the fibres of $\pi_\mP$ is a reasonable alternative to looking at the fibres of $\mP$.
The tracing index of $\mP$ is the degree of the map $\pi_P$, that is, the generic cardinality of $\pi_\mP^{-1}(p)$ for $p\in\VP$.
There is a dense subset of $\Ima(\mP)$ whose fibres by $\pi_P$ have cardinality equal to the tracing index of $\mP$.
Tracing index: example
$\mP=(t^2,\sqrt{t^2+1})$. Then $\VP=V(Y^2-X-1)$ and $\CP=\BP=V(\Delta^2-T^2-1,X-T^2,Y-\Delta,Z-1)$
Every point $(a,b)\in\VP$ with $a\neq0$ has two preimages in $\CP$, namely $T=\pm\sqrt{a}$, so the tracing index of $\mP$ is two.
On the other hand, $(1,\sqrt2)\in\VP$ has two preimages by $\mP$, but $(1,-\sqrt2)\in\VP$ has no preimage. Indeed, only half of the points of $\VP$ are covered by $\mP$.
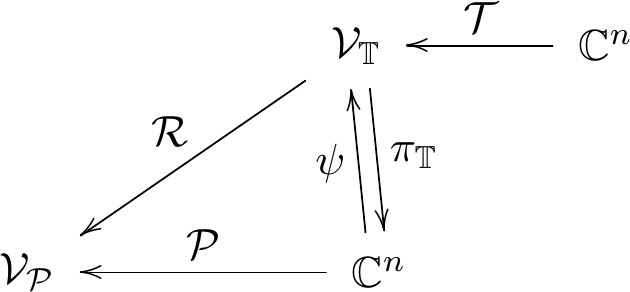
Tower variety
$\VT=\overline{\Ima(\psi)}$ also encodes relevant information
about the parametrization.
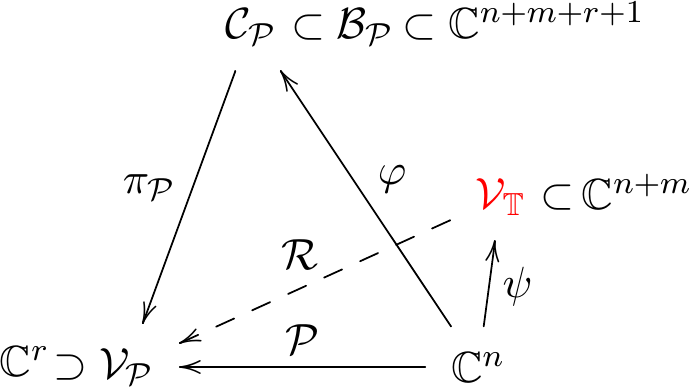
The radical map
\[\mP\colon\quad \C^n\rightarrow\VP\colon\quad\quad \OT\mapsto\overline{X}\]
is then "lifted" to the rational map
\[\mR\colon\quad \VT\rightarrow\VP\colon\quad (\OT,\overline{\Delta})\mapsto\overline{X}\]
$\VT$ has dimension $n$ and is contained in the zeroset of
$(\Delta_1)^{e_1}\cdot\alpha_{1D}(\OT) - \alpha_{1N}(\OT)$,
$(\Delta_i)^{e_i}\cdot\alpha_{iD}(\OT,\Delta_1,\ldots)-\alpha_{iN}(\OT,\Delta_1,\ldots)$
Properties in dimension one
\[ \mathrm{genus}(\VT)\geq\mathrm{genus}(\VP) \]
\[\ \Downarrow \]
\[ \VT \mbox{ rational curve} \ \Rightarrow\ \VP \mbox{ rational curve} \]
Additionally, if the tracing index of $\mP$ is one,
\[ \VT \mbox{ rational curve} \ \Leftrightarrow\ \VP \mbox{ rational curve} \]
Just by knowing which roots appear in a parametrization ($\VT$) you may be able to say things about the parametrization ($\VP$).
For example, any curve parametrized by rational functions in $t$ and $\sqrt[n]{t}$ is automatically rational, because $V(\Delta^n-T)$ is rational.
Properties in general dimension
Probably there are similar results
related to the plurigenera.
If the tracing index of $\mP$ is one,
\[ \VT \mbox{ rational} \ \Leftrightarrow\ \VP \mbox{ rational} \]
If $\VT$ is unirational, then $\VP$ is unirational. Furthermore, if $\mT(\ot)$ is a rational parametrization of $\VT$ then $\mP(\pi_\mathbb{T}\circ\mT(\ot))$ is a rational parametrization of $\VP$ where $\pi_\mathbb{T}(\OT,\overline{\Delta}) = (\OT)$.
Example
Let $\mP=\left(\sqrt[3]{t},\sqrt{1-\sqrt[3]{t^2}}\right)$.
$\VT=V(\Delta_1^3-T,\Delta_2^2-1+\Delta_1^2)$ is rational.parametrized as
\[ \mT(t)=\left( \left(\frac{2t}{1+t^2}\right)^3,\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2} \right) \]
We obtain the rational reparametrization
\[ \mP\left(\left(\frac{2t}{1+t^2}\right)^3\right) = \left( \frac{2t}{1+t^2},\frac{1-t^2}{1+t^2} \right). \]
Reparametrization algorithm
Assume that an algorithm that decides the existence
of rational parametrizations is known.
- INPUT: a radical parametrization $\mP$
- OUTPUT: one of
- A rational reparametrization of $\mP$
- "$\VP$ cannot be parametrized rationally"
- "No answer"
- Compute $\VT$ and parametrize it with the known algorithm.
- If $\VT$ is parametrized by $\mT(\ot)$ then
RETURN $\pi_\mathbb{T}\circ\mT(\ot)$. - If $\VT$ cannot be parametrized rationally, compute the tracing index $m$ of $\mP$. If $m=1$, RETURN "$\VP$ cannot be parametrized rationally", ELSE RETURN "No answer".
An application: integrals
$\displaystyle\int R(\sqrt[3]{t},\sqrt{1-\sqrt[3]{t^2}})\,dt$, where $R$ is a rational function, can always be converted by $u=\left(\displaystyle\frac{2t}{1+t^2}\right)^3$ into the integral of a rational function in $u$.
For example, $\displaystyle\int \frac{1}{\sqrt[3]{t}+\sqrt{1-\sqrt[3]{t^2}}}\,dt$ becomes the integral of a rational function in $u$ of degree 8.
A couple of questions
Under which conditions are $\BP$ and $\VT$ irreducible?
Under which conditions $\VT$ rational $\Leftrightarrow$ $\VP$ rational?